1.4 Diversité des supernovæ

Les techniques classiques de l'astrophysique sont essentiellement basées sur l'imagerie (ou photométrie, d'abord dans le domaine visible, puis radio, infra-rouge, ultraviolet, X et gamma), la métrologie (éphémérides, périodes de pulsation des étoiles variables, de rotation des systèmes binaires et de révolution des pulsars) et la spectroscopie qui permet de connaître la composition chimique et les propriétés physiques d'un corps par l'identification de l'empreinte des transitions énérgétiques mises en jeu pour modeler la densité spectrale d'énergie émise, communément appelée spectre.

La photométrie n'est en fait qu'une forme de spectroscopie à très basse résolution spectrale : on accumule l'énergie de l'ensemble des photons émis dans une large gamme de fréquence $\nu$ [s $^{-1}$ ] (donc d'énergie par photons E= $\hbar\nu$ [erg], ou de longueurs d'onde $\lambda$ =c/ $\nu$ [m]). On utilisera 3 filtres (bleu $\lambda$ =400nm, vert $\lambda$ =550nm et rouge $\lambda$ =700nm, couvrant le domaine visible) pour faire de la trichromie humanoïde. La bolométrie consiste à mesurer l'énergie totale, intégrée sur l'ensemble du spectre éléctromagnétique (spectroscopie à résolution nulle). Le domaine visible, profitant d'une bonne transparence atmosphérique et d'une technologie rôdée, est très usité.

1.4.1 Propriétés spectro-photométriques

Les courbes de lumière permettent de mesurer la luminosité et la couleur de l'objet, et donnent une indication de sa nature. Le spectre permet de classifier la supernova en fonction des éléments chimiques identifiés, suivant une classification historique (c.f. Figure 1.3) :

En l'absence d'Hydrogène, la supernova est de type I. Par ailleurs, en présence de Silicium, la supernova est de type Ia. En l'absence également de Silicium, mais en présence d'Hélium, la supernova est de type Ib. Enfin, en l'absence d'Hydrogène, d'Hélium et de Silicium, elle est de type Ic.

En présence d'Hydrogène, la supernova est de type II. Si le spectre est dominé par l'Hélium, elle est de type IIb. En présence de raies d'émission fines d'Hydrogène, elle est de type IIn. Enfin, du point de vue photométrique, on distingue en fonction de la courbe de lumière les supernovæ de type II-P qui présentent un plateau, et celles de type II-L qui présentent une décroissance linéaire.

Figure 1.3: Aspect shématique des courbes de lumières des supernovæ de type Ia, Ib/c, II-P et II-L (À gauche). Illustraction des raies spectrales permettant d'identifier les éléments présents dans la photosphère de supernovæ de type Ia, II et Ib/c (À droite) obtenues en 1999 (SN 1999ee et SN 1999ex ont explosées dans la même galaxie, la même année !).

Notons que le terme absence peut être interprété plus largement comme une faible présence (les SN-Ic présentent des raies de Silicium, mais bien plus faibles que les SN-Ia à une même phase). Aussi, d'éventuelles raies fines d'Hydrogène, provenant de l'interaction de l'éjectat avec le milieu circumstellaire précédemment soufflé par l'étoile, ne remettent pas en cause l'appartenance au type I, mais indiquent la présence d'Hydrogène circumstellaire (comme pour la SN-Ia 2002ic).

Selon notre compréhension actuelle, seules les SN-Ia sont des supernovæ thermonucléaires, tous les autres types étant des supernovæ gravitationnelles, qui laissent un objet compact en leur centre (comme pour la nébuleuse du Crabe, rémanent de SN1054, observée par les astronomes Chinois). L'absence d'Hydrogène ou d'Hélium dans le spectre des SN-Ib/c s'explique par la combustion et l'éjection de ces éléments légers au cours des stades terminaux de la vie de l'étoile.

1.4.2 Processus de formation des raies spectrales

Les raies spectrales qui modèlent les spectres de supernovæ correspondent aux transitions électroniques des ions présents dans le matériel entre la photosphère (la surface de dernière diffusion des photons, de profondeur optique $\tau$ unitaire) et l'observateur. En fait, la profondeur optique est différente en fonction de la longueur d'onde : à la longueur d'onde d'une transition électronique, la probabilité du photon d'être absorbée est plus élevée, donc la profondeur optique aussi. La photosphère à cette longeur d'onde sera plus externe. Elles sont décalées vers le bleu et élargies par effet Doppler car le matériel est en expansion rapide.

Dans un premier temps, l'éjecta est optiquement épais ( $\tau$ >1) aux longeurs des transitions électroniques. On observe alors des raies en absorption à ces longueurs d'ondes. On parle de phase photosphérique.

À mesure que l'éjecta s'etend et se dilue, sa profondeur optique diminue et la photosphère se déplace vers les couches plus internes. L'épaisseur de matériel intervenant augmente, sa composition change et intègre les éléments des couches plus profondes (si l'éjectat n'est pas uniformisé).

Finalement, la photosphère atteint l'objet central (ou dépasse le centre de l'éjectat dans le cas d'une SN-Ia). L'éjecta est transparent, et rayonne aux longueurs d'ondes des transitions électroniques, toujours excitées par le rayonnement dur de l'objet central et/ou par le rayonnement de désintégration des isotopes radioactifs formés lors de l'explosion. Le spectre de l'éjectat est donc constitué de raies en émission, et l'on parle de phase nébulaire.

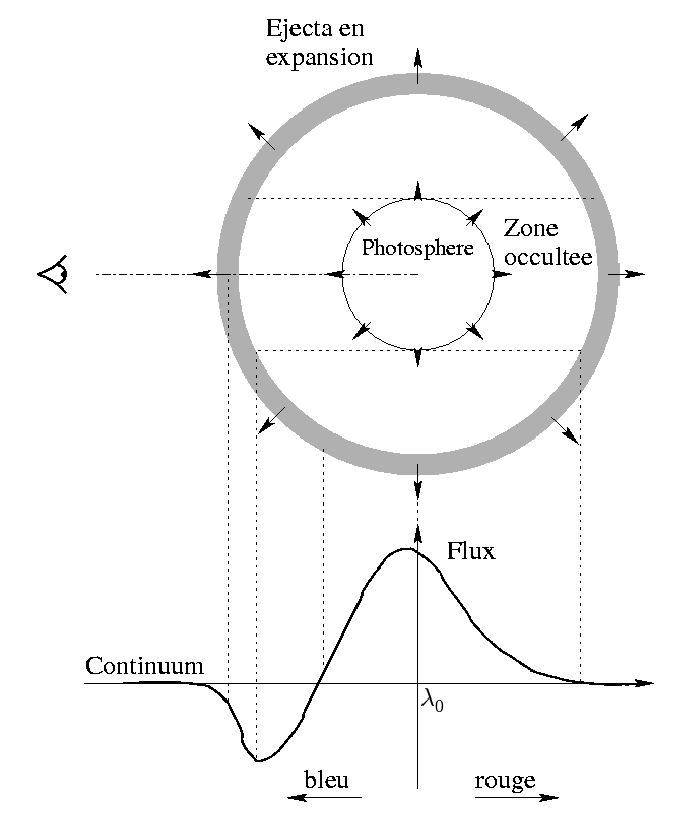
On constate sur la figure 1.3 que les raies de l'Hydrogène présentes dans le spectre de la SN-II ont une composante en absorption décalée vers le bleu, et une composante en émission. Ce type de profil est dit P-Cygni (du nom de l'étoile pour laquelle ils furent observés la première fois).

Pour expliquer le mécanisme de leur formation, il faut considérer la géométrie sphérique de l'éjecta : la partie qui masque la photosphère sphérique à l'observateur absorbe le rayonnement (exitation) et le renvoie dans toutes les directions (désexcitation). Le bilan sur le flux observé est une perte nette : ce rayonnement venait vers l'observateur, et une faible partie lui est renvoyée. Comme l'éjecta avance vers l'observateur, la raie est décalée vers le bleu.

À l'inverse, la partie de l'éjecta qui entoure la photosphère (en projection sur la ligne de visée) procède de même, mais le bilan est différent : la rayonnement absorbé n'aurait pas atteint l'observateur, mais une fois diffusé une partie lui parviendra. En fonction de la taille relative de la photosphère et de la coquille d'éjecta, et du profil de densité de ce dernier, la forme de la raie sera modifiée.

**Figure 1.4:** Schéma explicatif de la formation d'une raie P-Cygni par l'effet d'une coquille sphérique en expansion autour d'une photosphère. La partie qui masque la photosphère crée sur le continuum une raie en absorption décalée vers le bleu par rapport à la longueur d'onde $\lambda _0$ de la transition. La partie periphérique diffuse la lumière par fluorescence et forme une raie en émission dont le maximum est proche de $\lambda _0$ (la circonférence de la coquille projetée sur l'axe de visée est une caustique, et a une vitesse radiale nulle).

Les spectres de supernovæ sont essentiellement modelés par de telles raies P-Cygni, mais autour du maximum, pour les supernovæ de type I, l'opacité de l'éjecta rend la composante en émission très faible par rapport à la composante en absorption. À mesure que l'on s'approche de la phase nébulaire, la composante en émission devient dominante.

1.4.3 Standardisation des SN-Ia

Si, au regard des supernovæ gravitationnelles, la famille des supernovæ thermonucléaires est remarquablement uniforme, le temps a dévoilé l'existence de supernovæ apparentées à cette famille malgré de fortes dissemblances. L'année 1991 fut à ce titre révélatrice des limites de ce dogme avec l'observation de sn1991T, une magnitude plus puissante que la moyenne, puis de sn1991bg, une magnitude plus faible, qui sont depuis lors les prototypes des SN-Ia dites particulières, respectivement sur et sous lumineuses.

Sans considérer ces bornes extrèmes de la famille des SN-Ia, la dispersion de la luminosité au maximum dans la bande B est d'environ 0.8 magnitudes (soit un rapport de flux de deux entre les moins lumineuses et les plus lumineuses).

Pourtant, une corrélation a été découverte entre la luminosité au maximum dans la bande B (M

, $\lambda$ =450nm), et le taux de déclin de la luminosité : les SN-Ia les plus brillantes ont le taux de déclin le plus lent. C'est la relation de Phillips [12]. La mesure du taux de déclin d'une SN-Ia permet donc d'en déduire sa luminosité intrinsèque, comme la période le permet pour les Cépheïdes. La dispersion autour de la loi moyenne se réduit alors à environ 0.2 magnitudes (20% d'écart en luminosité).

Le taux de déclin peut être quantifié par la différence de magnitude au maximum et 15 jours après ( $\Delta$ m $_{15}$ ) ou par un paramètre de dilatation temporelle de la courbe de lumière (le strech s). Les deux approches donnent des résultats comparables. La masse équivalente de Ni $^{56}$ formé varie de 0.3 à 1 M $_{\odot}$ environ, une variation dont l'origine reste incertaine, mais provient vraisemblablement de différences physico-chimiques de la naine blanche (densité centrale, rapport d'abondance Carbone/Oxygène, qui modifient la fraction éléctronique et la vitesse de propagation de la flamme).

L'étude des couleurs des SN-Ia a également montré une grande homogénéité de l'évolution de (B-V) entre 30 et 90 jours après le maximum. L'amplitude du rougissement par les poussières interstellaires dans la galaxie hôte peut en être déduite, et l'absorption associée être corrigée [13]. La dispersion résiduelle en est encore réduite, à environ 0.15 magnitudes.

Du point de vue spectroscopique, une corrélation a également été trouvée entre le rapport $\mathcal{R}$ (SiII) de profondeur des raies du Silicium à 5750 et à 6100 Å et la magnitude au maximum dans la bande B [11].

La recherche d'un second paramètre capable d'expliquer cette dispersion résiduelle est toujours d'actualité, mais la communauté ne l'a pas attendu pour utiliser les SN-Ia comme des chandelles standardisables. Leur luminosité exeptionnelle les rend visibles jusqu'à des distances de plusieurs milliars d'années-lumières, et si la dispersion résiduelle de luminosité laisse une incertitude sur les distances qui en sont déduites, l'accumulation statistique d'événements peut théoriquement permettre de la réduire à volonté.

Une condition doit cependant être vérifiée pour ne pas obtenir une estimation de distance biaisée : c'est qu'il n'y ait pas d'effet d'évolution dans la relation de calibration. Il n'est pas déraisonnable d'imaginer que la métallicité du progéniteur ait un effet sur la luminosité de la supernova. Si cet effet ne suit pas la relation de calibration, qu'il y est orthogonal (par example, qu'à métallicité plus faible, pour un même taux de décroissance, la luminosité soit plus faible), alors les distances des supernovæ lointaines, de métallicité plus faible, seraient surestimées, mimant ainsi une accélération de l'expansion. Ce possible effet systématique est le principal argument des détracteurs de l'utilisation des SN-Ia comme indicateurs de distance. On peut leur opposer le fait que les SN-Ia ayant servi a calibrer la relation ont été observées dans des galaxies spirales et elliptiques, et couvrent donc déjà un grand intervalle de métallicités.

1.4.4 Des chandelles pour la cosmologie

Fort d'une nouvelle classe de chandelle standardisable, beaucoup plus lumineuse que les Céphéides, les astronomes ont pu mesurer des distances beaucoup plus grandes. La calibration de la luminosité intrinsèque des SN-Ia a été réalisée avec les SN-Ia proches, ayant explosé dans des galaxies pour lesquelles une mesure de distance a pu être obtenue par l'observation des Céphéides.

Le principal attrait de leur utilisation est de pouvoir mesurer la distance de galaxies lointaines, et en conjonction avec la mesure de leur décalage vers le rouge, de prolonger le diagramme de Hubble (traçant la distance en fonction du redshift, lié à la vitesse de récession) à des distances cosmologiques. Ce diagramme reflète la dynamique de l'univers, son taux d'expansion en fonction du temps, ce qui permet de confronter les modèles d'évolution cosmologiques aux observables.

Ainsi, la recherche de SN-Ia à grande distance par le High-Z SN search et par le SuperNovæ Cosmology Project a mis en évidence en 1998 l'accélération de l'expansion de l'univers, a réhabilité la constante cosmologique $\Lambda$ , et introduit la notion d'énergie noire.

La nature de l'énergie noire dépend de son équation d'état, qui relie sa densité $\rho$ et sa pression p (négative) via le paramètre d'état $\omega$ = p/ $\rho$ . Le modèle de constante cosmologique correspond à $\omega$ = -1. Les modèles d'énergie noire basés sur un potentiel scalaire (quintessence) permettent à $\omega$ de varier avec le temps ( $\omega$ < $\sim$ -0.8). Les cordes cosmiques mènent à $\omega$ = -1/3, les parois cosmiques à $\omega$ = -2/3. Pour $\omega$ <-1, on parle d'énergie fantôme.

Une mesure suffisamment précise du taux d'expansion en fonction du redshift, en particulier autour d'un redshift de 0.8, est à même de contraindre $\omega$ , et subséquemment de contraindre la nature de l'énergie noire.

Couplé aux mesures des anisotropies du rayonnement fossile (WMAP, qui contraignent la courbure de l'univers) et du pic acoustique des baryons par la fonction de corrélation des galaxies (SDSS, qui contraint la densité de matière), on s'approche d'une mesure précise du contenu énergétique de l'univers, ce qui constitue une réussite remarquable de la cosmologie observationnelle.

Le projet SNLS (SuperNova Legacy Survey) a été imaginé dans ce but de contraindre $\omega$ par l'observation de plusieurs centaines de SN-Ia à un redshift compris entre 0.2 et 1. La méthode de recherche classique de supernovæ consistant à suivre régulièrement une liste de galaxies a été abandonnée pour mettre en place une recherche glissante où un grand champ de 1 $^{\circ 2}$ est observé à intervalles de 4 jours, dans 4 filtres. On construit ainsi par empilement une image profonde de ce champ, qui sert à trouver les sources nouvelles par soustraction. Le SNLS est un volet du CFHTLS (Canada France Hawaï Telescope Legacy Survey), grand programme d'observations avec le CFHT, doté de la caméra grand champ MegaCam placée au foyer primaire, maintenant entièrement dévoué à ce programme heritage.

Les contraintes du SNLS étant fortes (bonne couverture temporelle pour pouvoir calibrer les courbes de lumières, observations successives dans différents filtres pour disposer des couleurs), il a obtenu la priorité sur les autre volets du CFHTLS (Shallow, Wide et VeryWide).

Enfin, et c'est ici que ma modeste personne entre en jeu, il est nécessaire de confirmer la nature des supernovæ observées, pour ne pas utiliser des SN-Ib/c ou des SN-II dans notre diagramme de Hubble. Pour cela, le SNLS a obtenu beaucoup de temps d'observation sur des téléscopes de la classe des 8 mètres afin de tirer le portrait spectroscopique des candidats prometteurs. Mon travail dans le groupe SNLS a essentiellement porté sur l'analyse des spectres obtenus sur l'instrument FORS1 du VLT.