Après ce travail préliminaire indispensable de calibration, on peut enfin passer au vif du sujet : l'extraction du signal spectral présent dans les images. Pour ce faire, il faut tout d'abord estimer le spectre du fond de ciel, invariant le long de la fente, le soustraire, puis calculer le flux restant à la position de l'objet.
On résume ainsi l'information bi-dimensionnelle contenue dans les images en un
simple vecteur F(
), représentant le flux associé à l'une des sources présente
dans la fente, pour chaque longueur d'onde échantillonnée le long de l'axe spectral.
Cette opération est implémentée dans un programme C++, extract, codé par le groupe du CEA-Saclay, et intégré dans le logiciel XspecSNLS. Deux méthodes d'extraction sont proposées : La technique d'extraction optimale de Horne [9], et une extraction de PSF à deux canaux, un point source et une source étendue. Cette dernière est utile lorsque la supernova est bien résolue par rapport à l'hôte.
Pour que la trace spectrale de l'objet ne soit pas sur les mêmes pixels déficients à chaque acquisition, le télescope est légèrement dépointé entre chacune d'elles, afin de déplacer la position de l'objet dans la fente. L'amplitude du dépointage est de 3'', soit 15 pixels sur le détecteur. Par exemple, pour une série de 5 acquisitions, la trace de l'objet se décalera de 15, 30, -15 et -30 pixels sur le détecteur. Ces décalages ne sont cependant pas toujours réalisés dans le même ordre.
Il faut donc préalablement inspecter les spectrogrammes (avec ds9 par exemple) pour determiner les décalages effectivement réalisés, grâce aux traces spectrales les plus brillantes. Ceci est parfois délicat lorsque le signal est faible, et qu'il n'y a pas d'autre objet présent dans la fente.
Ces décalages sont un des paramètres requis par le programme extract, ainsi que le nom des images réduites correspondantes.
Il faut également définir la position à laquelle le programme doit extraire l'objet (sur la première image, qui sert de référence), la largueur de la trace, et la fenêtre dans laquelle le niveau du fond de ciel sera estimé.
Encore une fois, ces paramètres sont définis visuellement sur les images, avec l'aide de la carte de pointage pour estimer la position relative de la supernovae par rapport à sa galaxie hôte. La largeur de la trace dépend de la qualité d'image durant l'acquisition, et la fenêtre d'estimation du fond de ciel est choisie de manière à éviter les sources présentes dans la fente. De même que pour le choix de la fente, la zone d'extraction doit être suffisement grande pour inclure tout le signal, mais la plus petite possible pour ne pas ajouter trop de bruit de lecture et de fond de ciel.
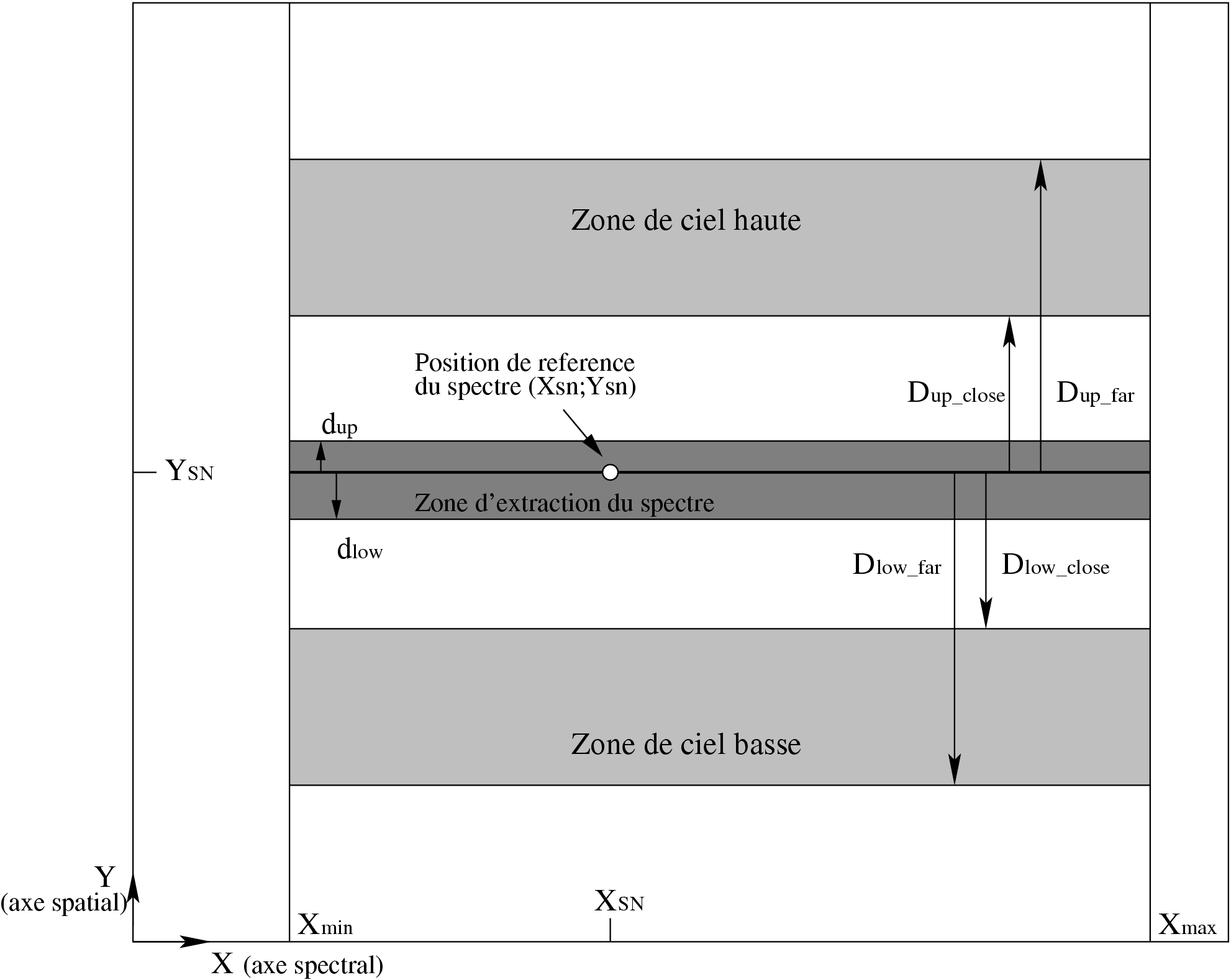
La définition des zones d'extraction se fait par 10 paramètres (c.f. Figure 2.5):
et 
, les coordonnées en pixels de la trace de l'objet.
et 
, le nombre de pixels au-dessus et au-dessous de
, entre lesquels le spectre sera calculé.
et
les bornes de la zone de ciel au dessus de l'objet.
et
les bornes de la zone de ciel au dessous de l'objet.
et 
, les bornes d'extraction.
|
|
Avec l'avènement des imageurs CCD et des grands téléscopes, les astronomes ont pu étendre leur domaine d'étude à des phénomènes auparavant inaccessibles. En 1986, Keith Horne tente de tirer le meilleur de spectres de la binaire serrée Z Cha, afin de déterminer ses paramètres orbitaux. Il s'avéra que l'algorithme standard d'extraction d'ouverture, qui additionne simplement le flux à l'intérieur d'une zone choisie, donnait des résultats trop bruités pour lui être utiles. Le bruit de lecture, du fond de ciel et les rayons cosmiques, participaient à dégrader le signal extrait.
Son diagnostic fut que les pixels contenant peu de signal ajoutent un bruit important
par rapport au signal gagné.
Il inventa donc une technique d'extraction optimale non biaisée,
où à chaque colonne (à chaque
), les pixels sont pondérés par la
fraction de lumière qu'ils doivent contenir (la valeur en ce pixel du profil spatial
normalisé, c.f. [9] Fig. 1).
Cette fraction est estimée, pour chaque ligne de l'axe spatial, par un ajustement polynomial,
en fonction de
, des fractions mesurées à chaque
.
L'inclinaison possible de la trace est donc prise en compte.
Les pixels déviant trop du profil attendu sont rejetés itérativement en tant
que rayons cosmiques.
Le gain pour des observations limitées par le bruit de fond est de 70% en temps
d'exposition effectif.
Cet algorithme fait l'hypothèse d'une source ponctuelle, non résolue, et d'un
profil spatial lentement variable avec
.
Si la seconde hypothèse est généralement vraie, nos objets sont fréquemment
des sources ponctuelles au sein d'une galaxie hôte. Le profil spatial de
la galaxie participera donc au calcul des fractions de lumière, et des poids assignés.
Pour éviter une trop grande contamination par le spectre de la galaxie, il faut limiter
au plus la largeur de la zone d'extraction.
L'extraction n'est alors plus optimale et devient biaisée, par la présence d'une
source résolue sous-jacente.
De nouveaux paramètres sont nécessaires au fonctionnement de l'algorithme :
le bruit de lecture, le gain et le niveau de réjection (en terme d'écart-type).
Le nombre de lignes à moyenner autour de
pour recalculer
, et
la largeur autour du
initial dans laquelle le maximum sera cherché,
actualisant
.
Lorsque la galaxie est résolue, on extrait également son spectre dans la zone symétrique par rapport au centre de la galaxie. On dispose ainsi d'une estimation du spectre galactique contaminant celui de la supernova, dans l'hypothèse où la galaxie est effectivement symétrique.