next up previous contents
Next: 2.4 Extraction du spectre Up: 2. Analyse spectroscopique en Previous: 2.2 FORS1 et moi

Sous-sections


2.3 Méthode de réduction

Dès que les observations sont effectuées, elles sont envoyées via le réseau à Garching (Allemagne), aux Quartier Généraux de l'ESO, où elles sont archivées. Nous pouvons les rapatrier depuis un site ftp, pour les réduire et les analyser au plus vite. La réduction nécessite d'autres images, appelées images de calibration, qui permettent de corriger des effets systématiques, et de calculer la fonction de sensibilité de l'instrument. Ces images sont prises pendant la journée, et ne sont disponibles qu'un peu plus tard. On dispose cependant des calibrations précédentes, que l'on peut utiliser en attendant de disposer des plus récentes.

Je vais décrire dans cette section la procédure de réduction, standard, suivie par l'équipe de spectroscopie en temps réel. Elle est implémentée dans le pipeline de réduction pour FORS1 de l'ESO, écrit en programme MIDAS (Munich Image Data Analysis System, développé par l'ESO).

Les personnes familières avec la réduction de spectres pourront survoler cette longue section. Mais à l'inverse, il est important de bien assimiler les concepts présentés ici pour la suite du manuscrit.

Une analyse critique de cette procédure à la lumière d'une description détaillée des sources de biais et de bruits propres aux capteurs CCD aboutira à la définition d'une procédure de post-analyse, dans le chapitre 3.

2.3.1 Pré-traitement des images

La première opération consiste à filtrer les images de science pour en retirer les impacts de rayons cosmiques. On utilise pour ce faire une routine MIDAS dédiée à cela : FILTER/COSMIC. Cette routine applique un filtre de Laplace à l'image. Ce filtre fait ressortir les brusques variations spatiales d'intensité, typiques des impacts. Les pixels dont le niveau dépasse de beaucoup le niveau de ses voisins sont remplacés par une interpolation polynomiale du niveau des voisins.

Il faut cependant définir le réglage du filtre, qui lui permet de quantifier l'écart au-delà duquel un pixel doit être rejeté. Le réglage s'effectue par trois paramètres au moins : le niveau du fond de ciel, le gain de détecteur et le bruit de lecture ( c.f. 2.3.2).

Le filtre est appliqué via l'invite de commandes de MIDAS, sur chaque image de science, et ce deux fois pour plus de robustesse (supprimer les « cratères » laissés par le premier filtre). Le filtrage d'une image sur un ordinateur moderne prend 5 secondes. Le niveau du fond de ciel est estimé visuellement avec ds9, le logiciel de visualisation d'images astronomiques au format FITS (Flexible Image Transport System), communément utilisé par la communauté des astronomes, et le gain et le bruit de lecture fournis par l'ESO dans l'en-tête de ces images FITS sont utilisés.


2.3.2 La cascade de réduction spectroscopique standard

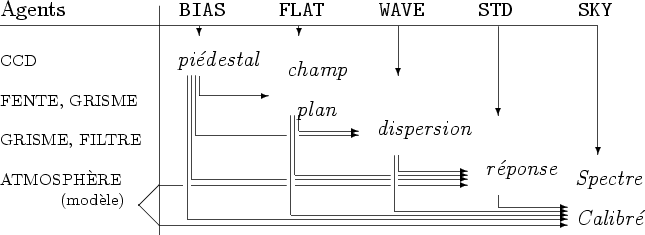
L'opération suivante consiste à corriger les images de science des irrégularités propres à la matrice du CCD. Cela s'effectue en deux étapes : premièrement par la soustraction du niveau minimum systématiquement présent, appelé niveau de biais ou piédestal. Puis par la correction de la variation de sensibilité pixel à pixel, en divisant par l'image de champ plan.

Figure 2.4: Schéma de la cascade de réduction. Les images de calibration (BIAS à exposition nulle, FLAT de lampe à incandescance, WAVE de lampe à arc et STD d'une étoile standard) permettent de modéliser le piédestal, la carte de sensibilité ou champ plan, la fonction de dispersion et la fonction de réponse instrumentale. Les modèles dépendent de certains agents intervenant dans la formation des spectrogrammes, et permettent de s'affranchir de leur effet. L'utilisation des quatre permet de calibrer les spectrogrammes de science (SKY).
\begin{figure}\begin{center} \begin{picture}(300,120) \put(-10,110){Agents} \p... ...(1,-1){10}} \put(70,5){\vector(1,0){205}} \end{picture} \end{center}\end{figure}

Calcul du piédestal :

Afin de connaître le piédestal, des images sont lues avec un temps d'exposition nul, à diaphragme fermé. Pour supprimer le bruit de lecture irréductible provenant du circuit électronique qui recueille et compte le nombre d'électrons excités dans chaque pixel, plusieurs réalisations de ces images sont moyennées.

On obtient ainsi une image du niveau de base du détecteur, qui dépend essentiellement de sa température. Elle sera soustraite systématiquement au début de la calibration de toutes les images. Il est donc important d'utiliser toujours la même image, ou le même modèle, afin d'être cohérent. La variance du niveau des pixels donne une estimation du bruit de lecture, référencé par ailleurs dans les en-têtes de chaque image, avec une valeur de 5.16 e-.

Calcul du champ plan :

La présence d'imperfections au sein du cristal semi-conducteur de silicium dopé, des poussières à sa surface, ainsi que des phénomènes d'interférences de couche mince à l'intérieur du cristal lorsque la longueur d'onde de la lumière incidente est proche de l'épaisseur du cristal, participent à dégrader localement la sensibilité des pixels. Il faut donc construire une image reflétant ces inhomogénéités afin de pouvoir les corriger.

Ceci est obtenu en éclairant uniformément le capteur, à un niveau suffisamment élevé pour rendre négligeable le bruit de lecture. Cependant, la configuration de l'instrument doit être identique à celle utilisée lors de l'acquisition des images de science, afin d'être comparable. Il faut en particulier que les pixels recoivent une lumière de même longueur d'onde, pour obtenir les mêmes franges d'interférences. Une illumination uniforme est alors obtenue, dans la direction spatiale, par une lampe à spectre continu (à incandescence), conjugée avec la fente d'entrée. En moyennant plusieurs images pour supprimer le bruit de photon ( bruit de grenaille ou de Poisson ), et en divisant par le spectre de la lampe estimé sur l'image moyenne, on obtient une image de champ plan normalisée, applicable là où le spectre de la lampe est grand par rapport au bruit de lecture.

.

La cosmétique du détecteur ainsi obtenue, en soustrayant le piédestal et en divisant par le champ plan, permet d'effacer les diverses tares du détecteur, et fournit une image codée en nombre corrigé d'unités lues, qui est un nombre réel, à la différence des images brutes, qui sortent du convertisseur Analogique-Numérique 16 bit sous forme d'entiers compris entre 0 et 65535 (2$ ^{16}$ -1). Chaque unité Analogique-Numerique (ADU) représente un certain nombre d'électrons effectivement présent dans un pixel. Le gain, défini comme le nombre d'ADU lus par e- présent, est également référencé dans les en-têtes des images, avec une valeur de 0.68 ADU/e-. Ces opérations constituent la calibration du détecteur CCD, qui tend à fournir l'image qu'aurait obtenu un détecteur parfait, dont tout les pixels auraient la même sensibilité.

Il ne reste alors qu'à interpréter ces images en terme de quantités physiques, c'est à dire à transposer les échelles de pixels en X et Y, et celles des ADUs, respectivement en échelles spectrale, angulaire et de flux : après s'être affranchi de la personnalité du seul détecteur, on doit s'affranchir de celle du reste de l'instrument. Ces opérations sont connues comme la réduction d'image, qui rend universelle une image provenant d'un instrument spécifique. La plus grande attention doit donc être portée à cette étape, sans quoi la comparaison quantitative d'observations est impossible. C'est l'une des sources d'incertitude les plus difficiles à corriger lorsque l'on travaille sur des observations prises par différents instruments, et réduites par différentes approches.

À l'inverse, en utilisant massivement un même instrument, comme on le fait ici, on peut obtenir un échantillon homogène réduit de manière identique.


Calibration en Longueur d'onde :

Si l'on s'occupe d'imagerie et non de spectrocopie, il faut, une fois la cosmétique du CCD réalisée, calculer la position et le flux d'étoiles dont les coordonnées célestes et la luminosité sont connues, dans le réferentiel des pixels. On peut ainsi définir la position des géodésiques célestes sur l'image, et calculer les coordonnées célestes et la luminosité de tout objet de l'image.

Dans le cas de la spectroscopie, une des dimensions du CCD ne correspond plus à une échelle spatiale, mais à une échelle spectrale.

Il est possible de connaître la loi assignant une longueur d'onde à chaque pixel en illuminant la fente d'entrée avec une lampe à arc, de spectre discret. Les fines raies d'émission des éléments composant le gaz à basse pression de la lampe sont séparées par le grisme et forment l'image de la fente sur le CCD, dédoublée autant de fois qu'il y a de raies. Il est alors facile d'associer chacune des longueurs d'ondes des raies d'émission, précisément mesurées en laboratoire, avec une des images de la fente (moyennant une hypothèse de monotonie).

Une telle image est prise en même temps que les images à exposition nulle et que les images des lampes à incandescence. Une fois calibrée du CCD, les raies isolées les plus intenses y sont identifiées, et leur trace est estimée le long de la dimension spatiale. Ces traces sont enfin modélisées par une loi polynomiale à deux variables ( coordonnées X et Y des pixels).

Dans le cas de FORS1 avec le grisme 300V et le collimateur standard, cette fonction de dispersion pour une fente centrée s'écrit grossièrement (c.f. section 3.4.3) :

$\displaystyle \lambda({\tt X},{\tt Y}) [\AA ] = \begin{array}[t]{ll\vert l} 5... ... \mbox{ aberrations optiques} \\ + 14 \; y^2 & - 16 \; x y^2 & \\ \end{array}$

avec $ x$ et $ y$ les variables réduites :

$\displaystyle x = \frac{{\tt X}-1040}{1024} \;\;; {\tt X}\in [1:2080] $

$\displaystyle y = \frac{{\tt Y}-1024}{1024} \;\;; {\tt Y}\in [1:2048] $

On peut alors rééchantillonner l'image selon une grille orthogonale de pas physique constant. La fonction de dispersion de la nouvelle image est ainsi linéaire : $ \lambda $ (X,Y) = 5880 + 2.65 ( X-1040 ) [Å], et ne depend que de la coordonnée X.

C'est à dire que l'image est corrigée des distortions optiques et que le pas des pixels est régularisé. Sa manipulation en est grandement simplifiée, dans la même mesure que la fonction de dispersion.

À l'axe Ydes pixels correspond la coordonnée angulaire le long de l'image virtuelle de la fente sur la voûte céleste, avec un pas que l'on estime constant, correspondant à l'angle imagé par un pixel de 24$ \mu $ m via un instrument de focale 25m : d$ \alpha $ = 24 10$ ^{-6}$ /25 rad $ \sim $ 0.2 ''. Les aberrations optiques sont ignorées, car on fait ici de la spectroscopie et non de l'astrométrie.


Calibration en Flux :

Maintenant que les pixels sont assignés aux coordonnées angulaires et spectrales, il faut pouvoir interpréter les ADUs récoltés par chaqu'un d'eux en terme de flux physique, dans une unité de mesure standard (F = h $ \nu$ [ergs/s] pour un photon de longueur d'onde $ \lambda $ = c/$ \nu$ ).

Idéalement, cette calibration en flux doit tenir compte des transmissions intégrées sur la ligne de visée entre l'objet d'interêt et le détecteur. Cela inclut :

  1. l'efficacité du détecteur (ADU/erg)
  2. la transmission du disperseur, du filtre, des lentilles du collimateur de FORS1 et la réflectivité des miroirs de l'UT utilisé
  3. la transparence de la colonne d'atmosphère traversée par le faisceau
  4. la diffusion par la poussière galactique dans le cas d'un objet extragalactique

On peut trouver dans la littérature des modèles ou des mesures de chacun de ces effets (efficacité quantique du CCD, réflectance du dépot d'aluminium des miroirs, diffusion atmosphérique de Mie, absorption par l'ozone, le dioxygène et la vapeur d'eau, carte de poussières galactique de Schlegel). Plutôt que de s'appuyer sur ces intermédiaires, il est plus direct d'observer une étoile brillante, dont le spectre est lisse et bien connu, et dont la constance semble assurée. L'ESO utilise une liste d'une soixantaine de ces étoiles standard spectro-photométriques, composée d'étoiles chaudes et de naines blanches. En fin de nuit, l'étoile standard la plus proche du zénith est observée dans chacune des configurations de FORS1 utilisées pendant la nuit.

Après avoir calibré cette image des effets du CCD et de la dispersion, la trace spectrale de l'objet est extraite, et comparée au spectre de référence correspondant. Leur rapport donne la fonction de réponse instrumentale, en ADU/erg/Å, en fonction de la longueur d'onde $ \lambda $ . Elle est propre au couple Grisme+Filtre ainsi qu'au détecteur et au télescope utilisé. Elle est en revanche indépendante de la fente utilisée.

Il faut distinguer lors de la calibration en flux les acteurs permanents et les acteurs variables. On s'attend à ce que la réponse instrumentale de l'instrument ne varie pas d'une lunaison à l'autre, alors que la transmission atmosphérique peut fluctuer à l'échelle du quart d'heure, le temps d'une pose. Il est par ailleurs intuitif que plus l'on observe loin du zénith, plus la colonne d'air traversée est grande, donc plus l'absorption atmosphérique est grande. Cet effet doit donc être corrigé indépendamment sur les spectres de standard et sur les observations de science si elles n'ont pas été prises à des angles zénithaux proches. Un modèle de spectre d'extinction atmosphérique E($ \lambda $ ) propre au site d'observation est appliqué, avec une dépendance exponentielle en fonction de la masse d'air traversée $ \mathcal{X}$ :

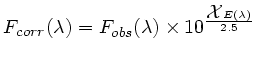
$\displaystyle F_{corr}(\lambda) = F_{obs}(\lambda) \times 10^{\frac{\mbox{$\mathcal{X}$}E(\lambda)}{2.5}} $

avec $ \mathcal{X}$ = sec($ \phi$ ), $ \phi$ étant l'angle zénital, et E($ \lambda $ ) exprimée en magnitudes absorbées par masse d'air.


2.3.3 Aspects techniques et implémentation

Quantité de Calibrations Disponibles :

Toutes ces opérations de calibrations doivent êtres effectuées dans l'ordre, puisqu'on a besoin des images de calibration précédentes pour calculer la suivante. Seule l'image du piédestal peut être obtenue à partir des seules données brutes. Le terme « cascade de calibration » englobe cet ensemble interdépendant d'opérations et de produits de calibration.

Deux cascades de calibrations peuvent choisir des approches différentes, qui aboutiront à des résultats finaux compatibles si elles sont correctes, mais l'une ne pourra utiliser les produits de calibration de l'autre. Par exemple, une différence du piédestal changera le contraste du champ plan : s'il est surestimé, le contraste augmente, mais d'autant moins que l'illumination est grande. Si l'illumination est trop faible, l'effet du bruit et de l'erreur d'estimation du piédestal peut mener à des valeurs négatives, aberrantes, du champ plan. Les impuretés profondes, où le détecteur est pratiquement aveugle, sont propices à de tels accidents. Et, à l'inverse, soustraire un piédestal trop faible donnera à ces impuretés une transparence usurpée au piédestal de lecture.

L'effet de cascade fait que pour obtenir une calibration fiable, il faut non seulement être capable de comprendre parfaitement les mécanismes participant à l'élaboration des images, mais aussi de disposer d'images de calibration brutes de bonne qualité. Et la qualité, quand on parle de statistiques, c'est aussi la quantité.

Les quotas d'images de calibrations dispensées par l'ESO aux utilisateurs du mode « service », sont de 5 images à exposition nulle, 5 spectrogrammes de lampe à incandescence, 1 spectrogramme de lampe à arc et 1 spectrogramme d'étoile standard.

Souvent, les étoiles standard sont observées avec une fente très large, de 5'', pour s'assurer que tout le flux de l'étoile est bien reçu, même si la qualité d'image est mauvaise ou que l'étoile est trop brillante pour l'utiliser comme étoile de guidage. Le mode multiobjet est utilisé, soit avec de larges fentes placées au centre soit à la même position que la longue fente à calibrer. Comme le spectrogramme de l'étoile n'apparaît que dans la fente centrale, les images ne sont lues que dans cette partie, au format 2048x400, au lieu de 2080x2048. Comme on utilise une configuration instrumentale différente, il faut construire les images de calibrations correspondantes. Donc l'ESO dispense également les 5 images nulles et les 5+1 spectrogrammes de lampes propres à la calibration de l'étoile standard : au format 2048x400.

Si l'on considère 5 observations par lunaison, prises des nuits differentes, en 5 expositions, cela représente 5x( (5+5+1)x2080x2048 + (5+5+1)x2048x400 ) = 55x2048x(2080+400) pixels de calibration. Soit 55 images de calibration de 2048x2480, plus 5 spectrogrammes de standard 2048x400, pour 25 spectrogrammes 2080x2048 des 5 objets. Soit 305 Mégapixels, ou 71 grandes images par mois. C'est également la taille d'une seule image de MégaCam.

Dans la pratique, l'ESO considère que le champ plan et la réponse instrumentale sont stable sur plusieurs jours, et ne répète pas forcément les observations d'étoile standard, ni de la lampe à spectre continu lorsqu'elles ont déjà été faites durant les nuits précédentes.

Mise en pratique :

Les routines MIDAS successives du Pipeline de FORS sont englobées dans une interface TcL-Tk réalisée pour la spectroscopie par la collaboration, qui permet avec quelques boutons d'effectuer l'ensemble de la cascade de calibration. Le jeu d'images de calibrations le plus récent est utilisé pour construire les références de calibrations et de réduction. Puis les images de science sont calibrées et réduites avec les références de calibration qui conviennent à leur configuration d'observation.

Il faut noter que l'étape de filtrage des rayons cosmiques peut se faire avant, pendant, où après la cascade. Il est fréquent qu'un rayon cosmique soit assez énergétique pour saturer son pixel d'arrivée, c'est à dire qu'il contiendra plus d'e- que le convertisseur ne peut en compter, et verra sa valeur assignée au maximum de 65563 ADUs. Pour peu que ce pixel ait par ailleurs une efficacité faible, la division par le champ plan démultipliera cette valeur, pouvant poser des problèmes de débordement numérique. L'histogramme des images brutes, ou des images réduites sans filtrage préalable, montre donc une grande dynamique, majoritairement créée par les impacts cosmiques. Or les logiciels de visualisation se basent sur cet histogramme pour assigner les niveaux de gris. Si un pixel est saturé et que l'on utilise une table de niveau de gris linéaire allant du minimum au maximum, qui est le mode par défaut de ds9, seul ce pixel sera visible en blanc, les autres étant indiscernablement noirs. Il faut redéfinir les bornes de la table des gris autour du niveau du fond de ciel pour visualiser le signal intéressant. Il a été décidé de filtrer systématiquement en premier lieu les images de science, dans un souci d'uniformité de la procédure de réduction. C'est sur ces images non rééchantillonnées que les impacts ont les bords les plus abrupts, et sont le mieux détectés. De ce fait, les images brutes codées en nombres entiers sur 16 bits passent à un codage en nombres réels sur 32 bits, avec un histogramme beaucoup plus étroit, avant d'êtres injectées au bas de la cascade de calibration, là où sont prêtes les références de calibration.

Les actions à effectuer pour produire les images réduites se résument en :

$ \star$
rapatriement par ftp des nouvelles images disponibles à Garching dans un nouveau répertoire.
$ \star$
lecture des en-têtes pour connaître la ou les configurations instrumentales utilisées
$ \star$
pour chaque configuration :

$ \bullet$
rassembler dans un nouveau repertoire les images correspondantes à cette configuration.
$ \bullet$
complétion si necessaire avec des images de calibration anterieures.
$ \bullet$
filtrage des cosmics avec MIDAS en mode interactif.
$ \bullet$
lancement de XspecSNLS pour effectuer la réduction :

-
organisation des données : listing des images et preparation des repertoires de travail (rawdata, redblock, calib, reduced).
-
reduction des images pour l'étoile standard :

  1. Calcul du modèle de piédestal
  2. Calcul du modèle de champ plan
  3. Calcul de la fonction de dispersion
  4. Calcul de la fonction de réponse instrumentale

-
reduction des images pour l'observation de science :
  1. Calcul du modèle de piédestal
  2. Calcul du modèle de champ plan
  3. Calcul de la fonction de dispersion
  4. Application des calibrations aux images de science

Le repertoire rawdata contient toutes les images brutes, redblock contient les fichiers MIDAS associant une action à un groupe d'images, calib contient les modèles de calibration et reduced contient les images réduites finales.

Le filtrage des impacts de rayons cosmiques, la construction des références de calibration et la calibration des images de science prend environ 15 minutes, lorsque tout va bien. L'étape la plus lente est le calcul du champ plan pour les images 2080x2048 (2 minutes pour 5 images).

Les en-tête d'images FITS :

La librairie logicielle eclipse de l'ESO offre des outils pratiques pour la manipulation des images FITS. Ainsi, on peut afficher l'en-tête complet de l'image FORS1_LSS106.fits avec la commande

$>dfits rawdata/FORS1_LSS106.fits
qui retourne 
 
====> file rawdata/FORS1_LSS106.fits (main) <====
SIMPLE  =                    T          / Standard FITS format (NOST-100.0)
BITPIX  =                   16          / # of bits storing pix values
NAXIS   =                    2          / # of axes in frame
NAXIS1  =                 2080          / # pixels/axis
NAXIS2  =                 2048          / # pixels/axis
ORIGIN  = 'ESO     '                    / European Southern Observatory
DATE    = '2004-04-15T01:31:10.481'     / UT date when this file was written
CRVAL1  =            150.08930          / value of ref pixel
CRPIX1  =               1031.0          / Ref pixel in x-axis
CDELT1  =         -0.000055626          / Increment in rows
CTYPE1  = 'RA---TAN'                    / Coordinate system of x-axis
CRVAL2  =              1.77105          / value of ref pixel
CRPIX2  =               1019.3          / Ref pixel in y-axis
CDELT2  =          0.000055626          / Increment in columns
CTYPE2  = 'DEC--TAN'                    / Coordinate system of y-axis
BSCALE  =          1.000000000          / pixel=FITS*BSCALE+BZERO
BZERO   =              32768.0          / pixel=FITS*BSCALE+BZERO
MJD-OBS =       53110.05462048          / MJD start (2004-04-15T01:18:39.209)
DATE-OBS= '2004-04-15T01:18:39.209'     / Date of observation
EXPTIME =             749.9697          / Total integration time
EXTEND  =                    F          / Extension may be present
OBJECT  = 'SN      '                    / Target description
INSTRUME= 'FORS1   '                    / Instrument used
TELESCOP= 'ESO-VLT-U1'                  / ESO Telescope Name
RA      =           150.089347          / 10:00:21.4 RA (J2000) pointing (deg)
DEC     =              1.77105          / 01:46:15.7 DEC (J2000) pointing (deg)
EQUINOX =                2000.          / Standard FK5 (years)
RADECSYS= 'FK5     '                    / Coordinate reference frame
LST     =            36671.950          / 10:11:11.950 LST at start (sec)
UTC     =             4719.000          / 01:18:39.000 UTC at start (sec)
ORIGFILE= 'FORS1_LSS106.fits'           / Original File Name
ARCFILE = 'FORS1.2004-04-15T01:18:39.209.fits' / Archive File Name
HIERARCH ESO OBS START       = '2004-04-15T01:02:08' / OB start time
HIERARCH ESO OBS EXECTIME    =         3441 / Expected execution time
HIERARCH ESO OBS TARG NAME   = 'SN      '   / OB target name
HIERARCH ESO TPL ID          = 'FORS1_lss_obs_off_fast' / Template signature ID
HIERARCH ESO TPL NAME        = 'Long slit observation with offsets along slit.'
HIERARCH ESO TPL NEXP        =            3 / Number of exposures within templat
HIERARCH ESO TPL EXPNO       =            1 / Exposure number within template
HIERARCH ESO TPL START       = '2004-04-15T01:17:39' / TPL start time
HIERARCH ESO DPR CATG        = 'SCIENCE '   / Observation category
HIERARCH ESO DPR TYPE        = 'SKY     '   / Observation type
HIERARCH ESO DPR TECH        = 'SPECTRUM'   / Observation technique

   [... suivi de 200 autres clef descripitives, dont : ]

HIERARCH ESO INS MODE        = 'LSS     '   / Instrument mode used
HIERARCH ESO INS COLL NAME   = 'COLL_SR '   / Collimator name
HIERARCH ESO INS GRIS1 NAME  = 'GRIS_300V'  / Grism name.
HIERARCH ESO INS FILT1 NAME  = 'GG435   '   / Filter i name
HIERARCH ESO INS SLIT WID    =         1.01 / slit width in arcsec
HIERARCH ESO INS SLIT POS      =       -12. / slit position in mm
HHIERARCH ESO DET OUT1 CONAD    =       1.46 / Conversion from ADUs to electrons
HIERARCH ESO DET OUT1 RON      =       5.16 / Readout noise per output (e-)
HIERARCH ESO DET OUT1 GAIN     =       0.68 / Conversion from electrons to ADU

   [...]
ce qui permet de savoir que cette image est la première image de science de trois prévues.

La commande dfits accepte le caractère Joker * pour lister l'en-tête de plusieurs images FITS, et va de pair avec fitsort qui permet de n'afficher que les clefs voulues :

$>dfits rawdata/FORS1*.fits $ \mid$ fitsort DPR.TYPE NAXIS1 NAXIS2 INS.GRIS1.NAME INS.SLIT.WID
renvoie 
 
FILE                                    DPR.TYPE        NAXIS1  NAXIS2  INS.GRIS1.NAME  INS.SLIT.WID
rawdata/FORS1_IMG_CAL105.5.fits         BIAS            2080    2048                                
rawdata/FORS1_IMG_CAL105.6.fits         BIAS            2080    2048                                
rawdata/FORS1_IMG_CAL105.7.fits         BIAS            2080    2048                                
rawdata/FORS1_IMG_CAL105.8.fits         BIAS            2080    2048                                
rawdata/FORS1_IMG_CAL105.9.fits         BIAS            2080    2048                                
rawdata/FORS1_IMG_CAL106.51.fits        BIAS            2048    400                                 
rawdata/FORS1_IMG_CAL106.52.fits        BIAS            2048    400                                 
rawdata/FORS1_IMG_CAL106.53.fits        BIAS            2048    400                                 
rawdata/FORS1_IMG_CAL106.54.fits        BIAS            2048    400                                 
rawdata/FORS1_IMG_CAL106.55.fits        BIAS            2048    400                                 
rawdata/FORS1_LSS106.1.fits             SKY             2080    2048    GRIS_300V       1.01        
rawdata/FORS1_LSS106.2.fits             SKY             2080    2048    GRIS_300V       1.01        
rawdata/FORS1_LSS106.3.fits             SKY             2080    2048    GRIS_300V       1.01        
rawdata/FORS1_LSS106.4.fits             SKY             2080    2048    GRIS_300V       1.01        
rawdata/FORS1_LSS106.5.fits             SKY             2080    2048    GRIS_300V       1.01        
rawdata/FORS1_LSS106.fits               SKY             2080    2048    GRIS_300V       1.01        
rawdata/FORS1_LSS_CAL106.1.fits         FLAT,LAMP       2080    2048    GRIS_300V       1.01        
rawdata/FORS1_LSS_CAL106.2.fits         FLAT,LAMP       2080    2048    GRIS_300V       1.01        
rawdata/FORS1_LSS_CAL106.3.fits         FLAT,LAMP       2080    2048    GRIS_300V       1.01        
rawdata/FORS1_LSS_CAL106.4.fits         FLAT,LAMP       2080    2048    GRIS_300V       1.01        
rawdata/FORS1_LSS_CAL106.5.fits         FLAT,LAMP       2080    2048    GRIS_300V       1.01        
rawdata/FORS1_LSS_CAL106.6.fits         WAVE,LAMP       2080    2048    GRIS_300V       1.01        
rawdata/FORS1_MOS_CAL106.10.fits        FLAT,LAMP       2048    400     GRIS_300V                   
rawdata/FORS1_MOS_CAL106.11.fits        WAVE,LAMP       2048    400     GRIS_300V                   
rawdata/FORS1_MOS_CAL106.6.fits         FLAT,LAMP       2048    400     GRIS_300V                   
rawdata/FORS1_MOS_CAL106.7.fits         FLAT,LAMP       2048    400     GRIS_300V                   
rawdata/FORS1_MOS_CAL106.8.fits         FLAT,LAMP       2048    400     GRIS_300V                   
rawdata/FORS1_MOS_CAL106.9.fits         FLAT,LAMP       2048    400     GRIS_300V                   
rawdata/FORS1_MOS_STD107.fits           STD             2048    400     GRIS_300V
et permet de vérifier qu'il ne manque pas d'image de calibration :

Un spectrogramme d'étoile standard (STD), 5 piedestaux (BIAS), 5 spectrogrammes de lampe à incandescance (FLAT,LAMP) et un spectrogramme de lampe à arc (WAVE,LAMP), tous au format 2048x400.

Plus 5 spectrogrammes de science(SKY) ainsi que les 5 BIAS, les 5 FLAT,LAMP et la WAVE,LAMP associées, au format 2080x2048, pris avec la même fente et le même grisme.

Cela illustre également la nomenclature qu'utilise l'ESO. L'instrument, le mode d'observation et éventuellement la catégorie de l'image forment le préfixe du nom de fichier. Le premier numéro dans le nom des images correspond au nombre de jours écoulés depuis le début de l'année, et le second au nombre d'acquisitions de ce type effectuées ce jour. Les jours ESO commencent à midi UT.

Les spectrogrammes MultiObjet (MOS) n'ont pas de clef INS.SLIT.WID car les 19 fentes peuvent avoir des largeurs differentes. Cependant, la clef SEQ.SPEC.TARG est introduite pour les calibrations prises en mode MOS mais reproduisant une configuration de longue fente (LSS). Il est ainsi possible de s'assurer que les spectrogrammes pris en mode MOS l'ont été dans la même configuration :

$>dfits rawdata/FORS1_MOS*.fits $ \mid$ fitsort DPR.TYPE INS.GRIS1.NAME SEQ.SPEC.TARG 
 
FILE                                    DPR.TYPE        INS.GRIS1.NAME  SEQ.SPEC.TARG
rawdata/FORS1_MOS_CAL106.10.fits        FLAT,LAMP       GRIS_300V       MOS_center   
rawdata/FORS1_MOS_CAL106.11.fits        WAVE,LAMP       GRIS_300V       MOS_center   
rawdata/FORS1_MOS_CAL106.6.fits         FLAT,LAMP       GRIS_300V       MOS_center   
rawdata/FORS1_MOS_CAL106.7.fits         FLAT,LAMP       GRIS_300V       MOS_center   
rawdata/FORS1_MOS_CAL106.8.fits         FLAT,LAMP       GRIS_300V       MOS_center   
rawdata/FORS1_MOS_CAL106.9.fits         FLAT,LAMP       GRIS_300V       MOS_center   
rawdata/FORS1_MOS_STD107.fits           STD             GRIS_300V       MOS_center
Ici, les fentes sont placées au centre du champ. Si elles avaient été placées à 18mm du centre, à la position de la fente de 1.31'', la clef vaudrait LSS_1.3_arcsec.

Produits finaux :

Une fois appliqués, les modèles de calibrations n'ont plus qu'un d'interêt consultatif ou complétif. Ils sont réunis dans le repertoire calib :


Tableau 2.3: Liste des modèles de calibration relatifs aux images de science produits par la chaîne de réduction MIDAS.
NOM DU FICHIER NATURE DU FICHIER
sci_masterbias_0000.fits Image modèle du piédestal
sci_normflat_0000.fits Image modèle du champ plan normalisé
sci_wave_0000.tfits Table des coefficients de la fonction de dispersion
instr_response_1D.fits Modèle de la fonction de réponse
atmext_1D.fits Fonction d'extinction utilisée pour calculer
  la fonction de réponse


On y trouve également les calibrations relatives à l'étoile standard, les divers produits de la chaîne de réduction (liste des pixels saturés par image par exemple) sous formes de tables FITS, ainsi que les notes de réduction.

Quant aux images de science calibrées et réduites, elles se trouvent dans le repertoire reduced. À chaque image FORS1_xxx.fits de type SKY correspond une image FORS1_xxx_0000.fits entièrement calibrée et réduite, et une image FORS1_xxx_0002.fits, calibrée du CCD et de la dispersion, mais pas de la réponse instrumentale.

next up previous contents
Next: 2.4 Extraction du spectre Up: 2. Analyse spectroscopique en Previous: 2.2 FORS1 et moi
Sylvain Baumont
2010-01-11