next up previous contents
Next: 3.5 Digression sur le Up: 3. Les promesses de Previous: 3.3 Propagation des erreurs

Sous-sections


3.4 Recettes de cuisine

Idéalement, pour contrôler au mieux les fluctuations instrumentales et atmosphériques, il faudrait acquérir plusieurs images de piédestaux avant chacune des acquisitions de science, et quelques spectrogrammes de champ plan, un de lampe à arc et un d'étoile standard avant et/ou après la série d'acquisitions de science. Ceci permettrait d'avoir une estimation du comportement de l'instrument au moment de l'observation. En mode service, les images de calibration sont prises en fin de nuit, et l'on devra s'en contenter.

Détaillons à présent les subtilités d'estimation des divers produits de calibration. Avant d'exécuter la modélisation, il faut définir la manière de grouper les images (par configurations identiques et par période de stabilité), et écrire les cartes ASCII descriptives de chaque groupe (avec Python). Les cartes sont alors lues par les routines C++ pour modéliser le produit de calibration dérivé de chaque groupe.

3.4.1 Une image de piédestal, d'accord mais pourquoi donc ?

Le capteur CCD dispose de 16 colonnes masquées de part et d'autre de la surface effective. Ce sont les régions de pré-lecture et de post-lecture. Ces régions permettent de mesurer directement le niveau du piédestal au cours de l'acquisition. Cependant, les images prises en mode MOS sont tronquées de ces régions (ce qui explique le passage de 2080 à 2048 pixels selon X). Elles le sont aussi des produits de calibration de la chaîne de réduction MIDAS. On utilisera alors le niveau de la région centrale comme référence. Cela permet de normaliser les piédestaux MOS entre eux, mais cette région étant exposée sur les autres types d'images, on ne pourra pas normaliser le modèle de piédestal à leur niveau.

Les modèles de piédestaux montrent que la bande centrale, où l'objet est imagé, est très uniforme (voir Fig. 3.3-b ainsi que les modèles présentés en Fig. 3.4).

Figure: À gauche : Fluctuation du niveau des régions masquées des images de piédestaux au cours de deux années. Le décrochage à 365 jours peut être imputé à une opération de maintenance. À droite : Niveau moyen de la bande centrale d'un modèle de piédestal MIDAS (visible en Fig. 3.4), estimé sur 200 lignes. La dispersion est d'environ 0.2 ADU localement, à comparer au bruit résiduel attendu de 5.4/(1.46 $ \sqrt {5}\sqrt {200}$ )=0.12 ADU dans une hypothèse d'ergodisme. Une tendance apparaît entre 0 et 300 pixels, zone généralement non illuminée en spectroscopie.
Image Scan_fullEvol Image Bias_Cut

La soustraction d'un piédestal uniforme ayant le niveau des régions masquées est donc une option valable, bon compromis entre le bruit résiduel ajouté (nul), et la précision de l'estimation (bonne globalement mais pas localement). Ceci n'est hélas pas praticable pour les observations en mode MOS, tronquées de ces régions masquées.

D'autre part, le calcul du piédestal est une bonne entrée en matière, pour se familiariser avec CFITSIO, tester les algorithmes de réjection des rayons cosmiques et valider la propagation des incertitudes. En effet, malgré un temps d'exposition nul, le temps de lecture de l'image suffit pour que des impacts aient lieu. L'absence de fond permet de tester la qualité de détection dans un cas favorable : la seule source de bruit est la lecture, dont l'écart-type est connu à priori.

Les images de piédestaux ont aussi le potentiel de fournir une mesure du bruit de lecture en chaque pixel. Son écart-type moyen est indiqué dans les en-têtes, mais on aimerait s'assurer qu'il est précis, et étudier l'uniformité pixel à pixel de ce bruit. L'absence de pixels chauds peut être vérifiée, et dans le cadre de la propagation des incertitudes, l'assignation d'un bruit de lecture propre à chaque pixel est un raffinement souhaitable.

Modélisation du piédestal :

Les seuls changements de configuration influant sur ces images sont la taille (NAXIS1 et NAXIS2), et le mode de lecture3.7(HIERARCH ESO DET OUT1 CLOCK). La forme du piédestal est très stable, car il découle des propriétés physiques des pixels et du circuit de lecture et d'amplification, isolés dans l'instrument. En revanche, le niveau moyen ($ \sim $ 200 ADUs) varie avec la température, à l'échelle de quelques ADU par nuit, d'une dizaine d'ADU par lunaison, et d'une cinquantaine d'ADU par an ( c.f. Fig. 3.3-a). L'intervalle de temps choisi pour créer les modèles est d'un trimestre (90 jours), compromis entre la réduction du niveau de bruit résiduel et validité des structures spatiales.

On considère que les piédestaux sont identiques à une constante près. Ainsi, on corrige les fluctuations du niveau des zones masquées par un coefficient additif appliqué à toute l'image. On construit de cette manière une série d'images que l'on espère stationnaire. Toutes les N images renormalisées ont un même niveau des zones masquées, et l'on peut appliquer notre moyenne robuste aux N réalisations indépendantes de chaque pixel, en supposant un niveau de bruit uniformément égal au RON fourni dans l'en-tête. Le bruit de lecture est indépendamment estimé en chaque pixel comme l'écart-type de l'échantillon validé. Ceci afin de construire une image du bruit de lecture susceptible d'être utilisée pour la suite de la calibration.

Figure: Comparaison d'une image brute de piédestal, et de modèles réalisés avec 5 (MIDAS), 25 (T3: Trimestre N$ ^\circ $ 3 ), 80 (T5: Trimestre N$ ^\circ $ 5 ) et 195 (Y2: Année N$ ^\circ $ 2 ) images. En haut : Images plein cadre (les régions masquées, plus sombres, se devinent aux bords de T3, T5 et Y2). En bas : Gros plans sur leurs régions centrales (200x200). À gauche :Comparaison des histogrammes résiduels de la région centrale des 5 images de piédestaux présentées. À droite : Graphique de l'effet du nombre d'images moyennées sur l'écart-type. L'écart-type d'une Loi de Poisson $ \sigma (N)=\frac {\sigma _0}{\sqrt {N}}$ tracé utilise les valeurs de bruit de lecture RON= 5.4 e- et de gain CONAD= 1.46 e-/ADU contenus dans l'en-tête de l'image brute pour définir $ \sigma _0$ = RON/CONAD=3.5 ADUs.
Image Raw_1 Image Mpb_5 Image Mlb_25 Image Mlb_80 Image Mlb_195
Image Raw_1_ctr Image Mpb_5_ctr Image Mlb_25_ctr Image Mlb_80_ctr Image Mlb_195_ctr
Image brute MIDAS (x5) T3 (x25) T5 (x80) Y2 (x195)
Image Bias_Histos Image RON_trend

En fonction du nombre d'observations, la quantité d'images de piédestaux disponibles varie (entre 15 et 80). Il est aussi possible de faire l'exercice sur l'ensemble des images d'une année (195 pour 2004). Comme on s'y attend, le niveau de bruit résiduel, estimé par l'écart-type spatial au centre de l'image (200x200, supposé ergodique) diminue en conséquence, suivant presque la prévision en $ \sqrt{N}$ (c.f. Fig. 3.4-droite). On observe également que l'on passe d'une image codée en nombres entiers à des valeurs de plus en plus résolues.

Les structures provenant d'interférences électroniques au cours de la lecture (visibles sur l'image (c) de la Fig. 3.4 ) ne sont pas statiques. Le modèle Y2 contient de nombreuses traces de telles structures, diluées par le moyennage. Elles contaminent cependant l'estimation du bruit de lecture, car l'hypothèse de stationnarité n'est plus vraie en présence de ces structures. Les histogrammes de l'écart à la moyenne dans la région centrale reflètent la diminution du bruit de lecture résiduel, et la présence de structuration (c.f. Fig. 3.4-gauche).

1er produit dérivé, l'image du bruit de lecture :

Dans le même temps que l'on moyenne les images pour construire le modèle de piédestal, l'écart-type des valeurs normalisées prises en chaque pixel pour toutes les images sert à construire une image du bruit de lecture.

Le format FITS permet d'ajouter plusieurs images ou tables à un fichier, en tant qu'extensions. L'image du bruit de lecture sera la première extension de l'image de piédestal, la seconde étant la table des pixels rejetés.

Ces images montrent que le bruit de lecture n'est pas identique pour tous les pixels : certains sont plus stables. L'amplitude des écarts reste néanmoins faible ( $ \Delta\sigma_{RON} \sim$ 0.5 ADU, c.f. Fig. 3.5). Dans certains cas, le bruit de quelques pixels s'écarte beaucoup de la valeur moyenne ( $ \sigma_{max} \sim$ 15). Comme ils ne sont pas systématiquement déviants, on ne peut les qualifier de pixels chauds, et les masquer sur chaque image. Ils sont rares, pas si aberrants, et l'on se contente donc de leur bruit plus fort, qui leur donnera un poids plus faible.

Figure 3.5: Gauche : Gros plan sur la région centrale de l'image du bruit de lecture du modèle T5. L'échelle de couleur va de 2.8 à 4.8 ADU. Droite : Histogrammes du bruit de lecture dans cette région, pour les 3 modèles T3, T5 et Y2.
Image Mron_80_ctr Image RON_Histos

2nd produit dérivé : la carte des rayons cosmiques :

La position et la puissance des pixels ayant été rejetés car trop déviants sont enregistrés au moment de leur détection dans une seconde extension de l'image de piédestal.

Pour vérifier le bon comportement de l'algorithme de réjection, on peut observer la répartition spatiale des pixels rejetés, et la distribution en puissance des impacts détectés.

Ceci apparaît en Fig. 3.6, pour le modèle T3,et l'on note une surdensité dans la partie haute de l'image. Étrange au premier abord, cela s'explique par l'effet du temps de lecture : les dernières lignes à être lues sont exposées plus longtemps et ont plus de chance d'êtres impactées.

La répartition en puissance montre que l'on ne détecte rien en deça de 17 ADUs (avec N $ \sigma_{RON}$ =5 x 3.5=17.5 ADUs, c'est normal). On rejette à peu près autant de pixels pour des déviations comprises entre 20 et 100 qu'entre 100 et 1000. L'aspect bimodal de la distribution peut s'interpréter comme la participation des ailes de la fonction de répartition au-delà de 5$ \sigma $ pour la partie basse, et celle des authentiques rayons cosmiques pour la partie haute.

Le taux de réjection vaut ici 6748/(25 x 2048 x 2048)=0.006 %, bien supérieur à la prévision de 0.00003 % pour une loi normale d'écart-type bien estimée, avec une coupure haute à 5$ \sigma $ . On sous-estime peut-être $ \sigma_{RON}$ , et la loi de répartition ne ressemble sûrement pas à une gaussienne. D'origine thermique et réduit à une poignée d'unités de lecture, le bruit suit une loi poissonnienne qui s'éloigne de l'approximation normale (c.f. Fig. 3.3).

Figure 3.6: À gauche : Carte des 6748 pixels rejetés lors de la création du modèle T3. Les pixels correspondant à une même image d'origine sont codés avec la même couleur (l'inverse est faux, il y a 5 couleurs et 25 images). À droite : Histogramme de puissance des impacts, en représentation Log-Log. Attention, les intervalles de comptage ne sont pas réguliers, mais suivent l'échelle logarithmique : le premier couvre $ \sim $ 1 ADU, le dernier en couvre $ \sim $ 700.
Image Bias25_Cosmic_Map Image Bias25_Cosmic_Histo

.

En conclusion, on dispose maintenant de modèles profonds de piédestal, dont le niveau de bruit résiduel est réduit à moins d'un ADU, et de modèles du bruit de lecture en chaque pixel. Le bruit dominant provenant plutôt du bruit de photon du fond de ciel, cette amélioration aura peu d'effet sur le rapport signal à bruit final. La fluctuation du niveau des zones masquées sert à normaliser les images.

3.4.2 La carte de sensibilité : quelle date de péremption ?

Ajoutons maintenant une illumination spectrale uniforme à ce piédestal, pour faire apparaître les variations de sensibilité pixel à pixel. Le temps d'exposition est choisi par les astronomes de l'ESO ($ \sim $ 9 sec.) afin d'approcher le niveau de saturation du CCD (65535 ADU) sans l'atteindre. Le bruit de lecture est alors négligeable devant le bruit de photons.

De nouveau, on réduit ce bruit en moyennant plusieurs acquisitions comparables. En plus de la taille et du mode de lecture, la configuration instrumentale importe : la position et la taille de la fente et le grisme utilisé modifieront les franges d'interférence. Le dépôt de poussières sur les optiques de champ et sur la fenêtre du capteur rompt la stationnarité et limite l'intervalle de temps de moyennage.

Il est envisageable de factoriser la carte de sensibilité en trois composantes : la transparence des pixels (stationnaire et blanche3.8), les franges d'interférences (stationnaires pour une configuration fente/grisme donnée) et la carte des poussières (non stationnaire).

On se limite pour l'heure à construire un modèle de champ plan par lunaison et par configuration. En effet, très peu de poussières se déposent en une dizaine de jours.

Figure 3.7: À gauche : Exemple d'un spectrogramme longue fente de lampe à incandescence. À droite : Spectre estimé sur des spectrogrammes obtenus avec différentes fentes.
Image RawFlat Image Slit_Effect

Normalisation par le spectre de la lampe :

Pour obtenir une sensibilité relative, le spectrogramme de la lampe à incandescence est divisé par son propre spectre. Il faut donc estimer celui-ci, mais sans connaître encore la sensibilité des pixels. C'est cette estimation qui définira la référence unitaire du champ plan.

La chaîne de réduction MIDAS procède à un moyennage glissant sur une région d'une centaine de lignes et quelques colonnes pour estimer le niveau d'illumination local. Cette méthode à l'inconvénient de sous-estimer l'illumination des zones de faible sensibilité étendues, et fait apparaître des fantômes dont la transparence est sur-estimée au-dessus et au-dessous des zones sombres (c.f. Fig. 3.8). À proximité de la coupure du filtre d'isolement d'ordre, où l'illumination passe rapidement de zéro à plusieurs milliers d'ADU, la sensibilité ainsi calculée n'est plus centrée sur l'unitée, mais décroît localement jusqu'à $ \sim $ 0.6 . Autre source d'étonnement : les trois dernières lignes sont à zéro !

Il faut aussi remarquer que l'homogénéité de l'illumination n'est pas parfaite : le profil spatial d'intensité de la lampe n'est pas strictement uniforme, le collimateur et les optiques introduisent un vignettage aux coins du champ, et la largeur de la fente n'est pas parfaitement constante (poussière obstructices, irrégularitées de découpe). Le vignettage et l'irrégularité de la fente seront aussi présentes lors des acquisitions de sciences et doivent donc apparaître dans le champ plan, mais l'intensité irrégulière de la lampe doit être corrigée. Il y a cependant une forte dégénérescence entre ces effets.

Dans un premier temps, j'ai utilisé l'algorithme de moyenne robuste pour estimer le spectre de la lampe dans des bandes de 200 lignes. Dans l'hypothèse où les variations de la lampe sont étendues, et que celles de la fente sont localisées, les spectres obtenus dans chaque bande sont interpolés linéairement en chaque ligne. On corrige ainsi en partie la variation d'intensité de la lampe, ainsi que le vignettage.

Néanmoins, en raison des termes en Y de la fonction de dispersion, l'interpolation dans les zones de fort gradient d'illumination entraîne un phénomène de crénelage3.9. Cela n'arrive qu'aux bords de l'image (c.f. Fig. 3.8), mais ce n'est pas très satisfaisant.

Pour corriger ce crénelage, il faut utiliser la fonction de dispersion. On ne l'a pas encore calculée (il est préférable de disposer du champ plan auparavant), mais elle n'a pas besoin d'être très précise ici. Un modèle moyen dérivé des fonction de dispersion calculées par MIDAS est utilisé (c.f. ci-après) : les spectres estimés dans chaque bande de 200 lignes sont transposés dans l'espace spectral, puis moyennés. On dispose ainsi d'une estimation globale du spectre de la lampe. Ensuite, pour chaque ligne, ce spectre est échantillonné selon les $ \lambda $ correspondant aux pixels, et la ligne est divisée par icelui.

On suppose donc que l'illumination est parfaitement uniforme, et le champ plan reflète à la fois le vignettage, l'irrégularité de la fente et les variations d'intensité de la lampe.

Figure 3.8: Comparaison des images de champ plan obtenues par MIDAS, en interpolant entre bandes, et en supposant une illumination uniforme. En haut : Images plein cadre, avec les mêmes coupures 0.95<f<1.05. En bas : Gros plans sur les détails évoqués : sur-estimation de part et d'autre d'une zone sombre, et sous-estimation au niveau de la coupure à 4150 Å par MIDAS (a), crènelage dû à l'interpolation linéaire au bord (b) et changement de régime de normalisation à 4150 Å (c).
Image Mpf_5 Image old_Mlf_10 Image Mlf_10
Image Mpf_ghostcut Image Mlf_aliasing Image Mlf_cut
(a) MIDAS (5 acq.) (b) Interpolé (10 acq.) (c) Uniforme (10 acq.)


Enfin, pour que la normalisation des champs plans de science pris en mode LSS et ceux des étoiles standard prises en mode MOS soient équivalentes, le spectre des lampes doit être estimé dans la même région du CCD. Le mode MOS 2048x400 généralement utilisé impose donc de calculer le spectre des lampes dans la bande centrale de 400 lignes des spectrogrammes LSS. Deux bandes de 200 lignes sont utilisées par défaut.

Moyennage des spectrogrammes :

La construction du champ plan comporte deux étapes indépendantes : la normalisation à l'unité, et le moyennage de plusieurs réalisations. L'ordre dans lequel ces deux opérations sont effectuées n'importe pas.

Comme l'estimation du spectre et le passage dans l'espace des $ \lambda $ est plus lent que le moyennage, on préfère moyenner d'abord et aplanir ensuite.

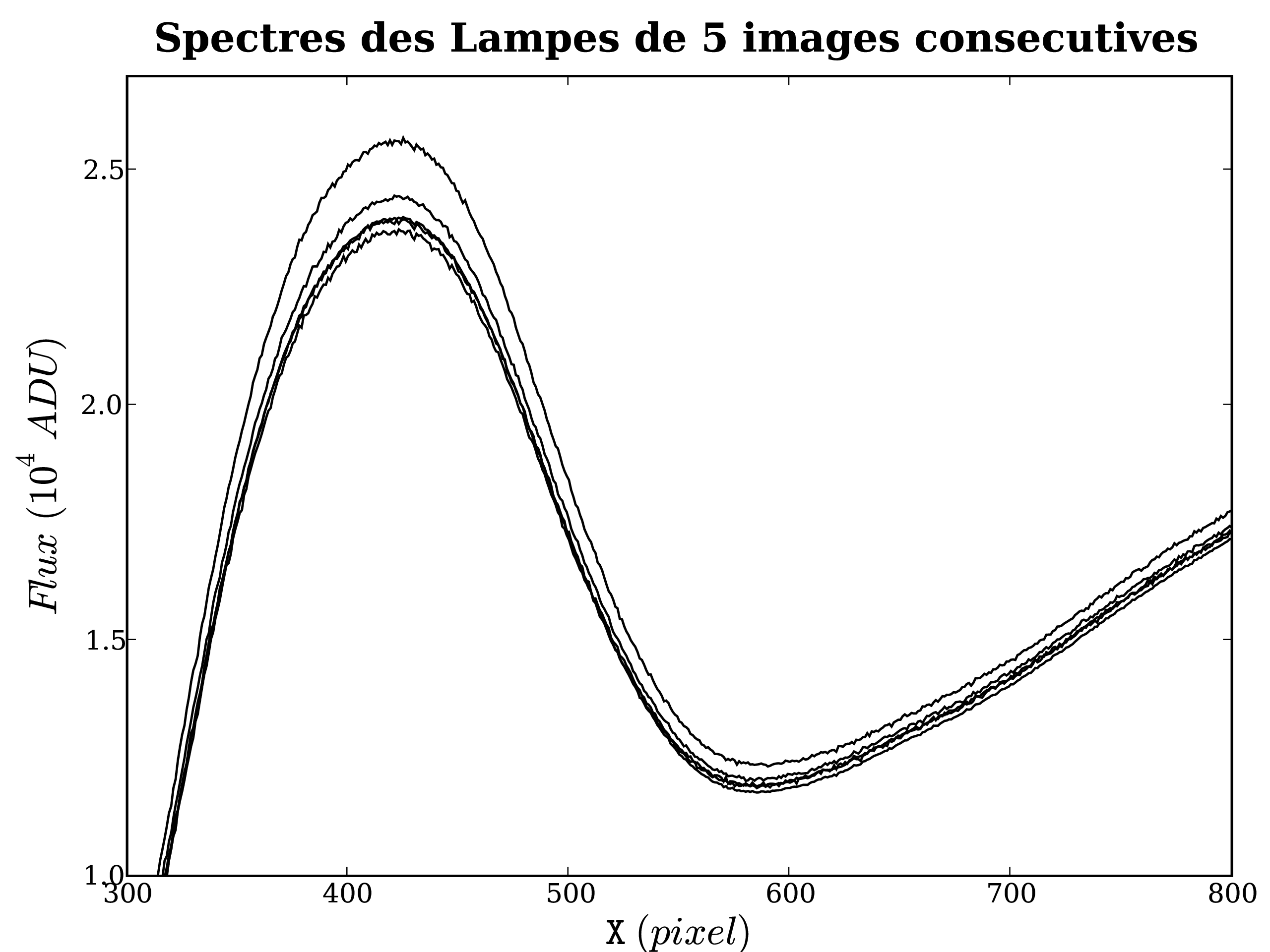
De même que pour le piédestal, il faut normaliser auparavant les spectrogrammes bruts pour les mettre tous au même niveau d'illumination. En effet, l'intensité de la lampe dérive asymptotiquement jusqu'à atteindre l'équilibre (c.f. Fig. 3.9). Lorsque la variation est trop importante, MIDAS invalide certaines images pour ne garder que les plus ressemblantes. Il arrive que 2 images sur 5 soient ainsi invalidées. On peut estimer l'intensité de multiples façons : dans une région centrale, selon une grille ou en une colonne par exemple. Il suffit d'utiliser le même estimateur pour tous les spectrogrammes.

En fait, pour bien illuminer l'ensemble de l'intervalle spectral, du proche UV au proche IR, l'ESO utilise deux lampes de températures différentes : FlatBlue et FlatRed, dont le maximum d'émmission se fait à 4600 Å et 7000 Å respectivement. Comme leur intensité varie indépendamment, il n'est pas possible d'utiliser un unique facteur de normalisation par image. Si l'on disposait de leur spectre bien mesuré et de la fonction de réponse, on pourrait se contenter de deux paramètres (un pour chaque lampe). Une analyse en composantes principales peut aussi permettre d'isoler les spectres de chaque lampe.

Image Lamp_Evol
Figure 3.9: Mise en évidence de la fluctuation d'intensité de la lampe FlatBlue au cours de 5 acquisitions de 8.7 secondes consécutives, à 2 minutes d'intervalle. Une variation de $ \sim $ 10 % apparaît ici.
 

On se contentera ici de calculer ce facteur en chaque colonne (à chaque $ \lambda $ ), comme le rapport entre le flux moyen de cette colonne pour une image et la moyenne $ F_{moy}$ (X) de ces flux moyens pour toutes les images.

Normalisées par ce facteur, les N images ont la même illumination moyenne en chaque colonne, et l'on peut appliquer l'algorithme de moyenne robuste aux N réalisations de chaque pixel, rejetant ainsi les impacts de rayons cosmiques, et réduisant le bruit de photons d'un facteur $ \sqrt{N}$ .

Les petits détails :

Il va sans dire que le modèle de piédestal normalisé au niveau des régions masquées de chaque spectrogramme est soustrait avant chaque estimation et avant le moyennage.

En deça de 4150 Å, le filtre d'isolement d'ordre absorbe les photons, et l'illumination ne provient que d'un peu de lumière diffusée. Elle ne suit pas la fonction de dispersion, et si l'on divise par son faible niveau, le bruit résiduel est énorme. 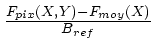On change donc de régime de normalisation en deça de 4150 Å, ainsi que dans les région masquées : la sensibilité $ f$ y est définie comme l'unité plus la différence entre le flux $ F_{pix}$ dans le pixel et le flux moyen $ F_{moy}$ de la colonne pour toutes les images, en terme du niveau moyen des régions masquées du piédestal $ B_{ref}$ : $ f$ (X,Y)=1 + $ \frac{F_{pix}(X,Y)-F_{moy}(X)}{B_{ref}}$ . Cette définition ad-hoc permet de garder la trace de la lumière diffusée, sans avoir de valeurs trop déviantes de l'unité.

Alors que l'on n'utilise qu'un modèle de piédestal par trimestre, on construit un champ plan par lunaison et par configuration utilisée, car 5 images suffisent pour obtenir un bon niveau de bruit. À quatre modèles de piédestal par an, s'ajoutent 24 modèles de champ plan par an, dans l'hypothèse où deux configurations différentes sont utilisées par lunaison. Et autant pour la calibration des étoiles standard prises en mode MOS. Le nombre d'images moyennées varie ici de 5 à 35. Le nombre d'étapes, les raffinements apportés et la taille des images rendent le temps de calcul du champ plan le plus important de toutes les modélisations. Pour 5 images LSS, il est d'environ une minute sur un poste de travail.

Figure 3.10: Comparaison des franges d'interférences obtenues aux grands $ \lambda $ , en fonction de la longue fente utilisée. Avec la fente de 1.0'', les longueur d'ondes sont plus élevées en une même position du CCD qu'avec la fente de 0.7'', et avec celle-ci qu'avec celle de 1.3'' (voir Fig. 3.7). Le code des couleurs et identique (de 0.95 à 1.05). On distingue quelques poussières fixes, qui diffusent la lumière autour d'elles, et de nombreux pixels sombres.
Image Fringe_10 Image Fringe_07 Image Fringe_13
Fente 1.0'' Fente 0.7'' Fente 1.3''

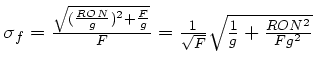Il est possible de construire une image du bruit statistique associée aux champs plans : pour une illumination $ F$ , le bruit résiduel normalisé de lecture et de photons s'écrit $ \sigma_f = \frac{\sqrt{(\frac{RON}{g})^2+\frac{F}{g}}}{F} = \frac{1}{\sqrt{F}}\sqrt{\frac{1}{g}+\frac{RON^2}{Fg^2}}$ . Pour un $ F$ supérieur à 10000 ADUs, en négligeant la composante du bruit de lecture, on trouve $ \sigma_f < \frac{0.01}{\sqrt{g}}$ , de l'ordre du pourcent. En combinant une dizaine d'images, on descend à quelques pour mille. L'effet propagé de cette incertitude sur un flux calibré $ F_0$ s'écrit $ \sigma_{fprop} = \sigma_f \frac{F-B}{f^2} = F_0\frac{\sigma_f}{f} \cong F_0 \sigma_f$ .

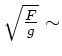Donc pour des flux de fond de ciel inférieurs à 100 ADUs par pixel, $ \sigma_{fprop}$ est inférieur à 1 ADU, et est petit par rapport au bruit de lecture ($ \sim $ 3.5 ADUs) et au bruit de grenaille ( $ \sqrt{\frac{F}{g}} \sim$ 10 ADUs). On négligera donc ce bruit propagé, économisant ainsi autant d'images de bruit résiduel qu'il y a d'images de champs plans.

.

Fort de ces modèles de calibration cosmétique de l'instrument, il est déjà possible de calibrer, soustraire du ciel et combiner les spectrogrammes de science, puis d'extraire le signal spectral. La calibration en longueur d'onde et en flux peuvent se faire après coup sur le spectre extrait (en ADU/pixel). N'anticipons pas et terminons de décrire la manière d'estimer la fonction de dispersion et la réponse instrumentale.


3.4.3 La fonction de dispersion : effets de flexion ?

On a vu que la fonction de dispersion est utile au calcul du champ plan, car tout spectrogramme en est affecté. Ceux de lampes à arc sont comparables à l'émission ionosphérique du ciel, peuplé de fines raies uniformes spatialement, mais qui apparaissent courbées de quelques pixels du haut au bas du CCD (c.f. Fig. 3.11). Les termes de distorsion sont donc essentiels pour soustraire les raies d'émission du ciel si le spectrogramme n'a pas été rééchantillonné pour corriger la distorsion.

Les fonctions de dispersion calculées par MIDAS permettent de construire un modèle moyen de cette fonction globalement stable. L'effet géométrique provoqué par le déplacement $ \Delta x_{foc}$ de la fente dans le plan focal peut être approximé par une dépendance linéaire des coefficients polynomiaux en X.

La variation de la longueur d'onde centrale peut d'ailleurs être anticipée :

$\displaystyle \frac{\Delta \lambda}{\Delta x_{foc}} = G_{coll} \frac{\Delta\la... ...x}} \simeq -0.23 \frac{2.65 [\AA /pix]}{24 [\mu m/pix]} \simeq -25 \AA /mm$

où $ G_{coll}$ est le grandissement du collimateur standard (estimé à partir de la focale effective de FORS1 en mode standard : $ f_{FORS}$ = $ \Delta x_{pix} $ / $ \Delta \alpha_{pix}$ = 24 $ \mu $ m/0.2'' $ \simeq$ 25m et de la focale $ f_{UT}$ des UTs, valant 108m. Donc $ G_{coll}$ = -$ f_{FORS}$ /$ f_{UT}$ $ \simeq$ -0.23) et $ \Delta\lambda_{pix}$ et $ \Delta x_{pix} $ sont la taille des pixels, respectivement en Å et en mm. Ainsi, l'échelle des $ \lambda $ augmente de $ \sim $ 300 Å entre la fente centrale de 0.28'' et celle de 1.0'' (à $ \Delta x_{foc}$ =-12 mm, c.f. Fig.3.7).

Les variations provenant de la flexion de l'instrument ne sont par contre pas facilement modélisables, mais elles sont d'amplitude beaucoup plus petite ($ \sim $ 1 Å durant une heure de suivi).

La solution de dispersion est un ajustement polynomial des positions des raies d'émission de la lampe à arc. La trace de chaque raie suit l'iso-$ \lambda $ correspondant de la fonction de dispersion (c.f. Fig. 3.11-a). Avant de pouvoir ajuster, il faut avoir détecté et associé le plus grand nombre de raies avec leur longueur d'onde mesurée en laboratoire. Le problème n'est pas trivial si l'on ne dispose pas déjà d'une solution approchée, qui fournisse la position à laquelle on doit s'attendre à trouver chaque raie. J'ai utilisé les fichiers de calibration en $ \lambda $ sci_wave_0000.tfits pour calculer une telle solution approchée.

Figure 3.11: À gauche : Spectrogramme brut des lampes à arc. À droite : Spectrogramme anamorphosé rendant visible la distorsion optique (haut). Profil d'intensité moyen central. Les raies d'émission utilisées pour l'ajustement polynomial de la fonction de dispersion sont identifiées (bas). Les echelles de couleur et d'intensité sont logarithmiques.
Image RawWave
Image RawWave_warp
Image Arc_Profil

Construction du modèle global de dispersion :

Les tables FITS produites et utilisées par MIDAS contiennent les 4 coefficients en X jusqu'à l'ordre 3, pour 80 positions selon Y :

$\displaystyle \lambda({\tt X})_{{\tt Y}_i}=C_{0,{\tt Y}_i}+C_{1,{\tt Y}_i}{\tt X}+C_{2,{\tt Y}_i}{\tt X}^2 +C_{3,{\tt Y}_i}{\tt X}^3 $

On trouve aussi dans l'en-tête, au format HISTORY spécifique à MIDAS, l'ensemble des coefficients en X, Y et XY (COEFSLIT1), le degré du polynome en X, Y et XY (NORMCOORD) ainsi que les origines et la normalisation (CENTERXY) définissant l'approximation polynomiale bidimensionnelle de la fonction de dispersion. En fouillant les routines MIDAS relatives à la dispersion ou avec un peu d'intuition, on decrypte le format des en-têtes de la façon suivante : 

>dfits calibs/sci_wave_0000.tfits
[...]
HISTORY  ESO-DESCRIPTORS START   ................
HISTORY  'COEFSLIT1','R*8',1,8,'3E23.15'
HISTORY    6.1473891799720E+03  2.7232378877427E+03  8.4196756656386E+01
HISTORY   -4.1598754221243E+01  3.9729174385012E-01  1.3467187732988E+01
HISTORY    6.1584631874311E-01 -1.5998412750378E+01
HISTORY
C0 Cx Cx2
Cx3 Cy Cy2
Cxy Cxy2 
HISTORY  'NORMCOORD','I*4',1,5,'7I10'
HISTORY           1         4         2         2         0
HISTORY
1 1+Ox Oy Oxy 
HISTORY  'CENTERXY','R*8',1,3,'3E23.15'
HISTORY    1.0310000000000E+03  1.0193000000000E+03  1.0240000000000E+03
HISTORY  [...]
$ X_0$ $ Y_0$ $ N_0$



Et la fonction de dispersion, approximée par un polynôme bidimensionel de degré $ Ox$ =3 en X, $ Oy$ =2 en Y et $ Oxy$ =2 en XY, fonction des variables réduites x= (X-$ X_0$ )/$ N_0$ et y= (Y-$ Y_0$ )/$ N_0$ s'écrit :

$\displaystyle \lambda(x,y) = C_0 \begin{array}[t]{lllc} + C_{x} x & + C_{x2} ... ...+ C_{y2} y^2 & & [Oy] \\ + C_{xy} xy & + C_{xy2} xy^2 & & [Oxy] \end{array}$

Un programme Python se charge de lire ces 8 coefficients dans les en-têtes de toutes les tables produites par MIDAS, ainsi que les paramètres de configuration de l'instrument (grisme et position de la fente). Les fonctions de dispersion sont réécrites pour une origine ($ X_0$ ,$ Y_0$ ) commune, autorisant leur comparaison, et moyennées par lunaison.

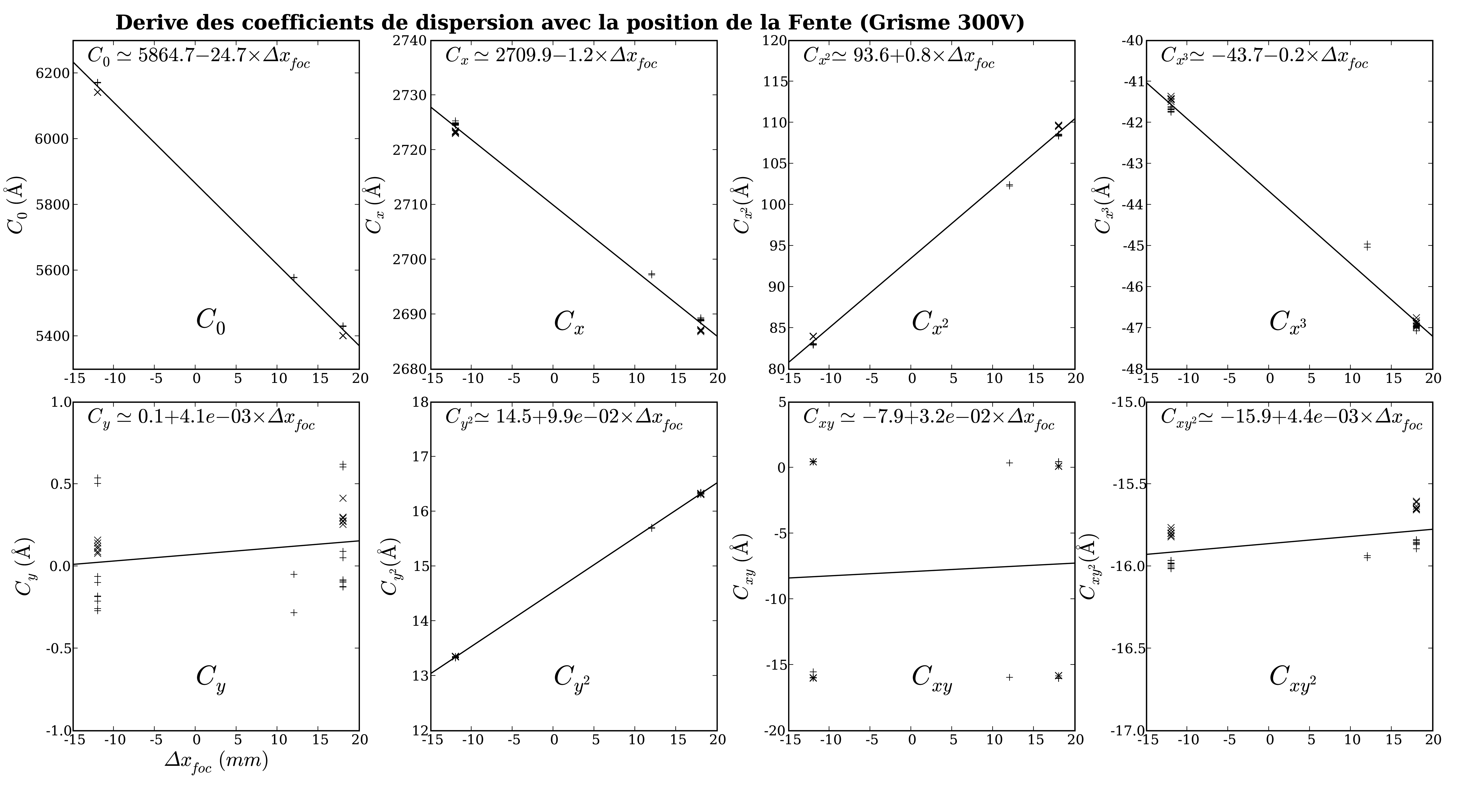
Un ajustement linéaire des coefficients en fonction de la position $ \Delta x$ de la fente permet de définir un modèle global de dispersion (c.f. Fig. 3.12). Dans le cas du grisme 300V monté sur l'UT1, au vu des ajustements présentés en figure 3.12, le modèle retenu serait :

$\displaystyle \begin{array}[t]{lll\vert ll\vert ll} C_0 (\Delta x) & = 5865.0 ... ... C_{x3} (\Delta x) & = -43.7 & - 0.2 \Delta x_{foc}\quad & & & & \end{array}$

où les coefficients sont exprimés en Å et $ \Delta x_{foc}$ en mm. L'origine est choisie à ($ X_0$ ,$ Y_0$ ) = (1040,1024) et la normalisation est conservée à $ N_0$ = 1024. Le terme d'inclinaison $ C_y$ est globalement nul. Le terme croisé $ C_{xy}$ présente un instabilité suspecte, et sera considéré nul. L'écart fréquent des coefficients mesurés pour la fente de 0.7'' est révélateur de la limitation intrinsèque du model : il n'est précis que dans l'espace couvert par les observations : 30 avec les fentes 1.0'' et 1.3'', et 2 avec la 0.7''. $ C_{y^2}$ est stable et corrélé avec la position de la fente, mais suffisamment peu pour que cela soit négligé.

Figure 3.12: Ajustement linéaire des coefficients de dispersion calculés par MIDAS, en fonction de la position $ \Delta x_{foc}$ de la fente. Seules les dispersions en mode longue fente et avec le grisme 300V, prises entre Juillet 2003 et Janvier 2005, moyennées par lunaison, sont utilisés ici. 3 positions de la fente y sont présentes : -12 (1.0''), 12 (0.7'') et 18 (1.3'') mm. Les mesures prises sur l'UT1 sont marquées $ +$ , celles sur l'UT2 $ \times $ .
Image dslit_Mid_Cdisp

Ce modèle moyen, approximatif, ne prétend pas résoudre le problème de la dispersion, mais simplement guider les algorithmes de détection et d'identification des raies d'émission, qui fourniront un modèle précis pour un spectrogramme de lampe à arc donné. Considérer simplement 6 coefficients polynomiaux et une correction :

$\displaystyle \lambda(x,y,\Delta x) = C_0-25\Delta x_{foc} + C_x x + C_{x2} x^2 + C_{x3} x^3 +C_{y2} y^2 + C_{xy2} x y^2 $

serait assez précis pour trouver facilement les raies d'émission. Il sera affiné par la suite, lorsque l'on disposera de nos propres solutions de dispersion.

Identification des raies d'émission de lampes à arc :

La fonction de dispersion sera d'autant mieux contrainte que le nombre de raies est grand, et que leur répartition est régulière. Pour augmenter le nombre de raies d'émission, l'ESO allume simultanément plusieurs lampes à arc contenant des gaz de compositions différentes (Hélium, Mercure/Cadnium et Argon). Leurs acronymes sont listés dans les en-têtes : 

 
HIERARCH ESO INS LAMP1 NAME  = 'He+1    '   / Name of the lamp switched on
HIERARCH ESO INS LAMP2 NAME  = 'HgCd+2  '   / Name of the lamp switched on
HIERARCH ESO INS LAMP3 NAME  = 'Ar+1    '   / Name of the lamp switched on
HIERARCH ESO INS LAMP4 NAME  = 'Ar+2    '   / Name of the lamp switched on
Le Manuel de Référence de FORS1+23.10contient la liste des 100 principales raies excitées, dont voici la longueur d'onde des plus intenses et isolées, en Å dans l'air (et non dans le vide), et en fonction de l'ion émetteur :
Hg I He I Ar I  
3650.144 3888.6460 6965.4307 8667.9443
4046.557 4471.4790 7147.0415 9122.9678
4358.343 4921.9312 7383.9805 9224.4990
5460.742 5015.6797 7635.1060 9354.2197
  5875.6211 7723.9844 9657.7803
  6678.1509 8264.5225 9784.5000
  10830.2998 8521.4424  
Ces valeurs ont étés comparées aux valeurs tabulées dans les fichiers de calibration de MIDAS et d'IRAF, ainsi qu'aux valeurs prédites par la théorie quantique, calculées par R.L. Kurzuc3.11. Des écarts de l'ordre de 0.01 Å apparaissent parfois, et peuvent provenir de raies multiples, mélangées, de limites instrumentales ou de conditions physiques differentes. Les valeurs MIDAS ont été utilisées, car sûrement plus adaptées à l'instrument. Comme $ C_0$ peut varier de $ \sim $ 50 Å (de l'UT1 à l'UT2), et que l'estimation de leur position est biaisée par les raies voisines, ces raies sont sélectionnées pour être les raies les plus intenses dans un intervalle de 50 Å. Les raies mélangées, faibles ou trop proches l'une de l'autre sont retirées (c.f. Fig. 3.11).

Disposant d'un modèle approximé de dispersion, et des longueurs d'ondes d'émission des ions des lampes, on peut prévoir l'abscisse X de chaque raie. Le spectrogramme brut des lampes à arc est calibré du piédestal et du champ plan, et moyenné selon Y dans 9 bandes. Les spectres obtenus sont filtrés par convolution avec une ondelette dite du chapeau Mexicain, adaptée à la détection de profils rectangulaires ayant la largueur projetée de la fente (5 pixel/''). Le maximum local le plus proche de la position attendue de chaque raie est ajusté par une parabole pour calculer la position exacte de la raie (c.f. Fig. 3.13).

Figure 3.13: Illustration de la technique de détection et de mesure de la position des raies d'émission. L'ondelette s'étend sur 4 fois la largeur supposée L = 5 pixels des raies, et est normalisée pour que sa convolution avec un rectangle unitaire de largeur L vaille 1 au maximum. Son intégrale est nulle par construction. Le doublet du mercure à 5770 et 5791 Å est résolu, mais le filtrage mène à sous-estimer $ \lambda _{rouge}$ et à sur-estimer $ \lambda _{bleu}$ .
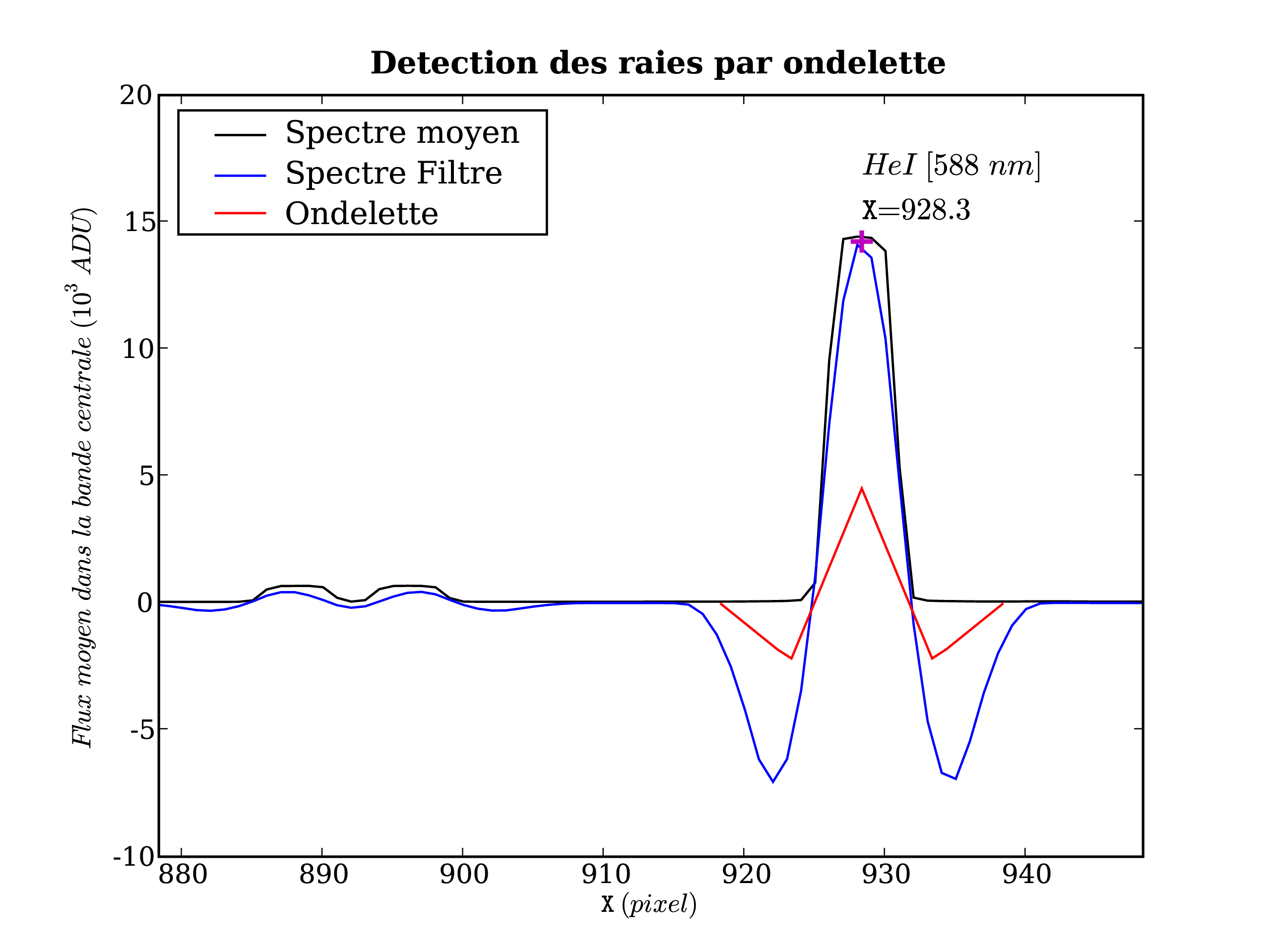
Image ArcHe_ID

Résolution des équations de dispersion par les moindres carrés :

A présent, on connaît l'abscisse $ {\tt X}_i$ d'une dizaine de raies, pour 9 ordonnées $ {\tt Y}_j$ différentes. Les coefficients polyonmiaux reproduisant au mieux ces positions sont calculés par la méthode des moindres carrés (minimisation du $ \chi ^2$ ) : On assigne à chaque raie $ \lambda_i$ un poids $ w_i$ arbitraire d'autant plus grand que la raie est intense et isolée. Les ordres (k,l) de la loi polynomiale de dispersion P(x,y) sont définis, et l'on cherche à déterminer la valeur des coefficients polynomiaux $ C_{k,l}$ à partir des 126 mesures indépendantes x$ _{i,j}$ , et connaissant les 14 $ \lambda_i$ et les 9 Y$ _j$ choisis comme références. Ce problème est linéaire en fonction des coefficients, et la minimisation du $ \chi ^2$ équivaut à une inversion de matrice :

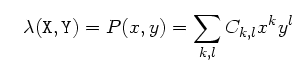soit$\displaystyle \quad \lambda({\tt X}, {\tt Y}) = P(x,y) = \sum_{k,l} C_{k,l}x^k y^l$    le modèle de dispersion,

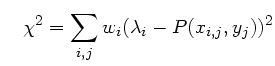et$\displaystyle \quad \chi^2 = \sum_{i,j} w_i (\lambda_i - P(x_{i,j},y_j))^2$    le résidu des mesures au modèle.

Pour chaque coefficient $ C_{k,l}$ , le $ \chi ^2$ est minimal lorsque sa dérivée seconde par rapport à $ C_{k,l}$ s'annulle :

$\displaystyle \begin{array}{rcl} \forall C_{k,l} & : & \frac{\delta \chi^2}{\d... ...'} y_j^{l+l'} \right] = \sum_{i,j} w_i x_{i,j}^k y_j^l \lambda_i \end{array} $

Ce qui s'écrit sous forme de produit matriciel, dans le cas où $ C_{1,2}$ est le dernier coefficient polynomial :

$\displaystyle \hspace{-1.5cm} \left[ \begin{array}{ccccc} \sum_{i,j} w_i & \cdo... ...bda_i \vdots \\ \sum_{i,j} w_i x_{i,j} y_j^2 \lambda_i \end{array} \right] $

$\displaystyle \Leftrightarrow \bf { A \times X = B } $

$\displaystyle \Rightarrow \bf { X = B \times A^{-1}} $

Ainsi, le calcul de $ \bf {A}$ , de son inverse $ \bf {A^{-1}}$ et de $ \bf {B}$ permettent de calculer la matrice colonne $ \bf {X}$ des coefficients polynomiaux. Le problème est bien posé tant que l'on dispose de plus de mesures que d'inconnues. $ \bf {A}$ est alors définie positive, et inversible. Avec \begin{displaymath}(k,l) \in \begin{array}[c]{\vert c\vert c\vert} \begin{array... ...array}{c} 0,1 0,2 \hline 1,1 1,2 \end{array}\end{array} \end{displaymath} , soit 8 inconnues, on est assuré d'obtenir une solution.

La résolution en $ \bf {X}$ de $ \bf { A \times X = B }$ est implémentée dans la librairie lapack3.12 (cholesky_solve(A,B)), mettant en \oeuvre la méthode d'inversion de matrices symétriques, définies positives, inventée par André-Louis Cholesky (1875-1918), précisément pour résoudre des problèmes de minimisation de $ \chi ^2$ en topographie.

Afin de réduire à une fraction d'Å les résidus à la fonction de dispersion (c.f. Fig. 3.14), j'ai été amené à augmenter l'ordre $ Ox$ du polynôme en X à 4.

Figure 3.14: En haut : Écarts entre un modèle de dispersion linéaire : $ \lambda $ (X,Y)=$ C_0$ + $ C_1 \times $ x et les longueurs d'onde des 14 raies identifiées, dans 9 régions. La composante polynomiale résiduelle indiquée est tracée en gris. En bas : Idem, mais avec le modèle de dispersion complet à 9 paramètres $ \lambda $ (X,Y) = P(x,y) ajusté par les moindres carrés. Les résidus sont tracés en fonction de X$ _{i,j}$ à gauche, et en fonction de Y$ _j$ à droite.

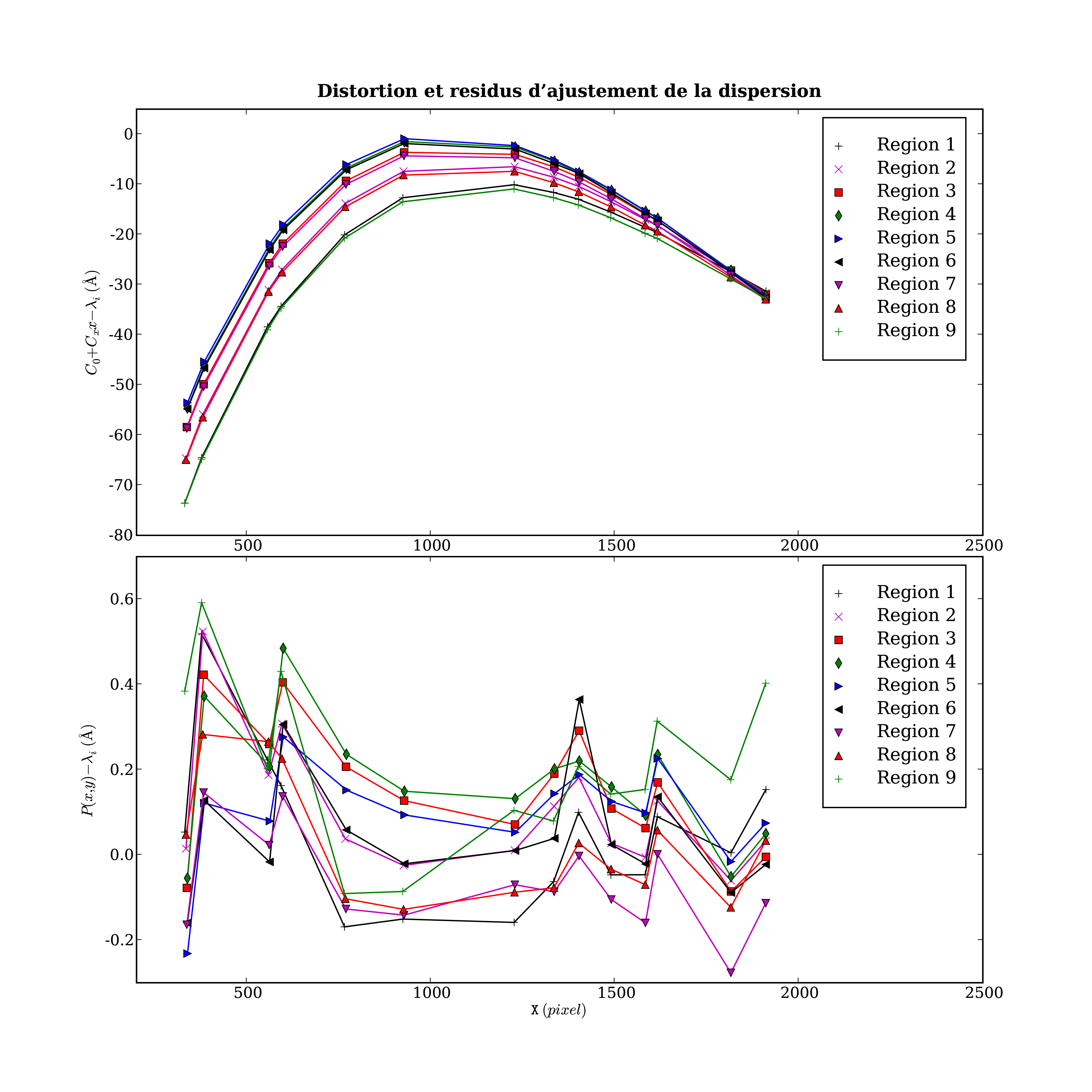
Image Arc_Residu

Le modèle global obtenu en ajustant linéairement ces nouveaux coefficients en fonction de la position $ \Delta x_{foc}$ de la fente pour le grisme 300V devient (c.f. Fig. 3.15) :

$\displaystyle \begin{array}[t]{lll\vert ll\vert ll} C_0 (\Delta x) & = 5865.0 ... ... \Delta x_{foc} & & & & \\ C_{x4} (\Delta x) & = 13.0 & & & & \\ \end{array}$

Figure 3.15: Ajustement linéaire des nouveux coefficients de dispersion, en fonction de la position $ \Delta x_{foc}$ de la fente. Seules les 88 dispersions en mode longue fente et avec le grisme 300V, prises entre Juillet 2003 et Janvier 2005, sont utilisées ici. 4 positions de la fente y sont présentes : -24 (2.5''), -12 (1.0''), 12 (0.7'') et 18 (1.3'') mm.

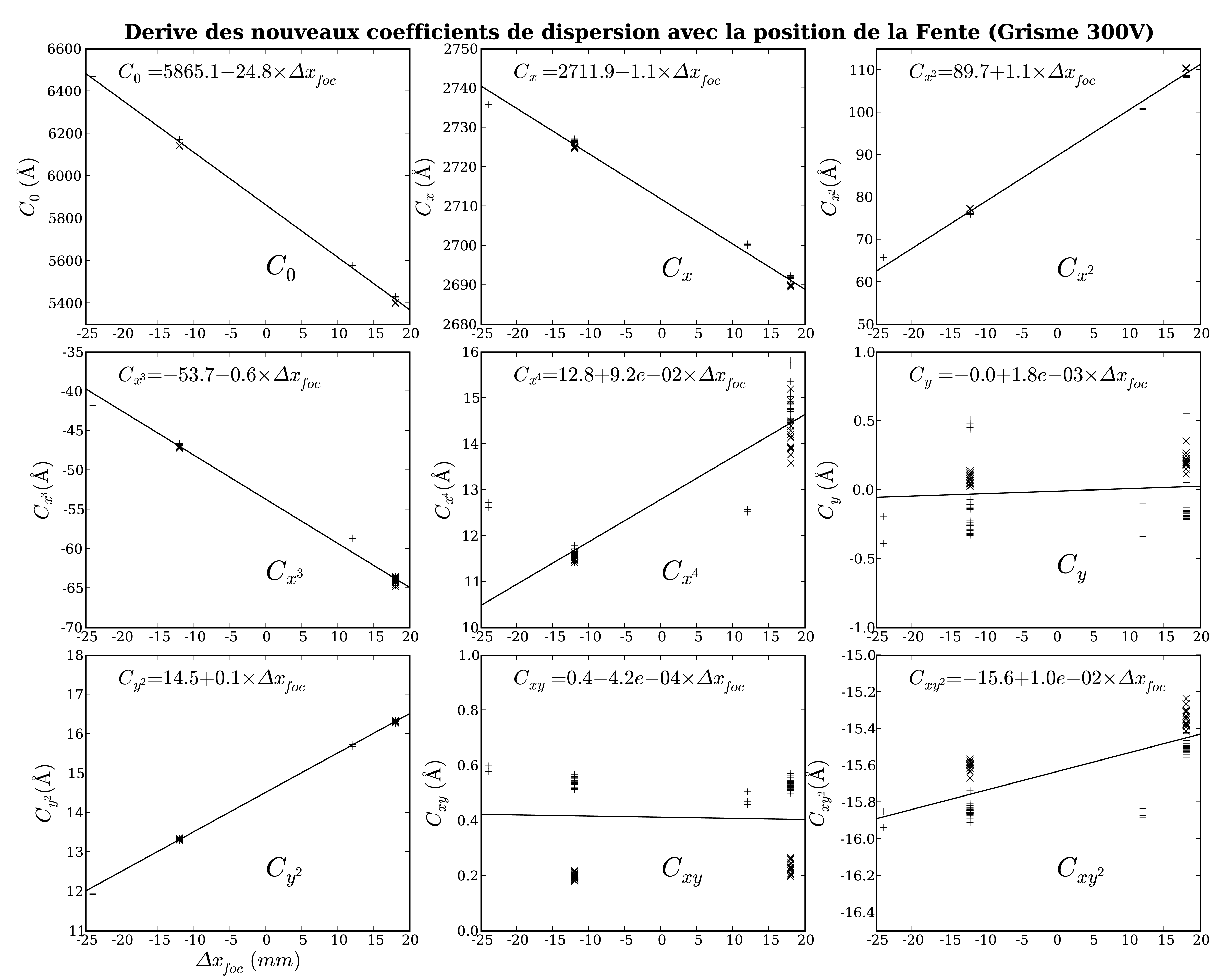
Image dslit_off_Cdisp

On atteint une dispersion résiduelle à chaque ajustement d'environ 0.2 Å, équivalent à $ \sim 0.1 pixel$ . Trois sources d'incertitudes y participent :

$ \bullet$
L'imprécision des $ \lambda_i$ de référence,
$ \bullet$
L'imprécision de l'estimation de la position $ {\tt X}_{i,j}$ des raies, combinaison
-
de la pixelisation
-
du moyennage robuste selon Y
-
de l'estimation du centroïde par ondelette
$ \bullet$
Les ordres supérieurs de la fonction de dispersion réelle.

La précision de la calibration en $ \lambda $ sera supposée égale à 0.2 Å, ce qui est largement suffisant pour obtenir un redshift précis à mieux que 10 $ ^{-4} \times$ (1+z) dans notre gamme de $ \lambda $ (de 4000 Å à 9000 Å). La flexion et la torsion présentes au cours des acquisitions de science seront corrigées (via $ C_0$ et $ C_y$ ) en identifiant l'émission de OI ionosphérique à 558 nm.

Arnaché de tout les attributs de calibration que l'on puisse obtenir sans ouvrir le dôme, l'heure est venue du baptême du feu : l'observation d'une étoile de référence.


3.4.4 La fonction de réponse instrumentale :

Il ne reste plus en effet qu'à estimer la fonction de réponse instrumentale pour pouvoir calibrer entièrement les spectrogrammes. Rappelons que la factorisation de la sensibilité des pixels en champ plan $ f$ (X, Y) et réponse instrumentale $ \mathcal{R}(\lambda)$ rend ces deux modèles de calibration inter-dépendants.

Si l'on connaissait le spectre exact $ \mathcal{L}(\lambda)$ des lampes à incandescence, on pourrait déduire $ \mathcal{R}(\lambda)$ du spectre moyen $ L_{moy}(\lambda)$ utilisé pour normaliser le champ plan :

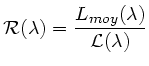
$\displaystyle \mathcal{R}(\lambda) = \frac{L_{moy}(\lambda)}{\mathcal{L}(\lambda)} $

La factorisation serait alors parfaite : les éventuelles colonnes sombres du détecteur lavées par la normalisation apparaîtraient dans la réponse intrumentale. Cependant, la réflectivité des miroirs et la transparence de l'atmosphère seraient absentes de la fonction de réponse.

La factorisation serait aussi parfaite si l'on observait une étoile standard à la même position et avec la même configuration que les acquisitions de science, et si aucun filtrage n'était réalisé sur le spectre extrait ou sur la fonction de réponse calculée. L'ESO n'observa les étoiles standard en mode LSS que jusqu'en Janvier 2004 (14 obs). Ensuite, seul le mode MOS, souvent centré, fut utilisé pour les étoiles standard, avec des ouvertures larges de 5''.

Comme $ \mathcal{R}$ ne dépend théoriquement que de $ \lambda $ (les autres dépendances patiales doivent être dans le champ plan), on peut le calculer, pour un couple grisme+filtre donné, à n'importe quelle position de la fente. La calibration en $ \lambda $ permet de passer de l'espace des pixels à celui des $ \lambda $ , d'abord lors du calcul de $ \mathcal{R}(\lambda)$ , puis avant la division par $ \mathcal{R}(\lambda)$ calibrant en flux les spectres de science.

Ceci n'est valable que tant que la couverture spectrale du spectrogramme de l'étoile standard contient celle des acquisitions de science. Si les observations de science sont réalisées avec la fente 1.0'', alors que l'étoile standard est observée avec une fente centrée, l'intervalle [8600,8900]Å sera sur les spectrogrammes de science mais pas sur celui de la standard.

L'\oeil de MIDAS:

Pour introduire les facteurs influants sur la fonction de réponse, auxquels j'ai été confronté durant cette ultime étape de calibration, je vais présenter ici la méthode suivie et les fonctions de réponse produites par MIDAS.

Les spectrogrammes d'étoile standard sont calibrés du CCD et en $ \lambda $ , la trace de l'étoile est calculée, et le flux en chaque colonne, en chaque $ \lambda $ , est estimé par un ajustement de PSF (point spread function : fonction d'étalement du point). L'extinction atmosphérique est corrigée en utilisant la masse d'air enregistrée dans l'en-tête et un modèle d'extinction (celui du voisin Cerro Tololo Inter-American Observatory, CTIO).

Le spectre obtenu est comparé aux spectres de référence disponibles, leurs coordonnées aussi, et l'étoile est ainsi identifiée. Les transmissions, la réflectivité et l'efficacité quantique composant la fonction de réponse sont lisses, donc cette dernière le sera aussi. Pour s'affranchir du bruit de photon et autres incertitudes, le spectre est intégré dans des intervalles de 50Å, et le spectre de référence aussi. Les bandes d'absorption tellurique et les raies d'absorption photosphériques notables (O2 et H2O pour l'atmosphère terrestre, HI pour celle des étoiles) sont exclues. Le rapport de ces flux intégrés fournit une centaine de points égaux à l'intégrale de $ \mathcal{R}(\lambda)$ dans l'intervalle de $ \lambda $ considéré.

La fonction de réponse finale est calculée comme étant une fonction de spline s'ajustant aux points intégrés. Le résultat est incontestablement lisse, mais présente parfois un comportement aberrant aux bords (c.f. Fig. 3.16). En particulier, la coupure brutale dans le bleu ne peut l'être autant dans l'espace des spline. Le second ordre de diffraction et l'absence de contrainte laissée par le masquage des raies telluriques de H2O dans le rouge laissent parfois le spline remonter.

Figure 3.16: Superposition des 35 fonctions de réponse de FORS1 sur l'UT1 produites par MIDAS. Les réponses pour une même configuration (mode,grisme,filtre,fente) sont tracées d'une même couleur. La legende résume le mode, le grisme et la longue fente utilisée ou reproduite (ctr correspond au centre, ou à la fente 0.28'').

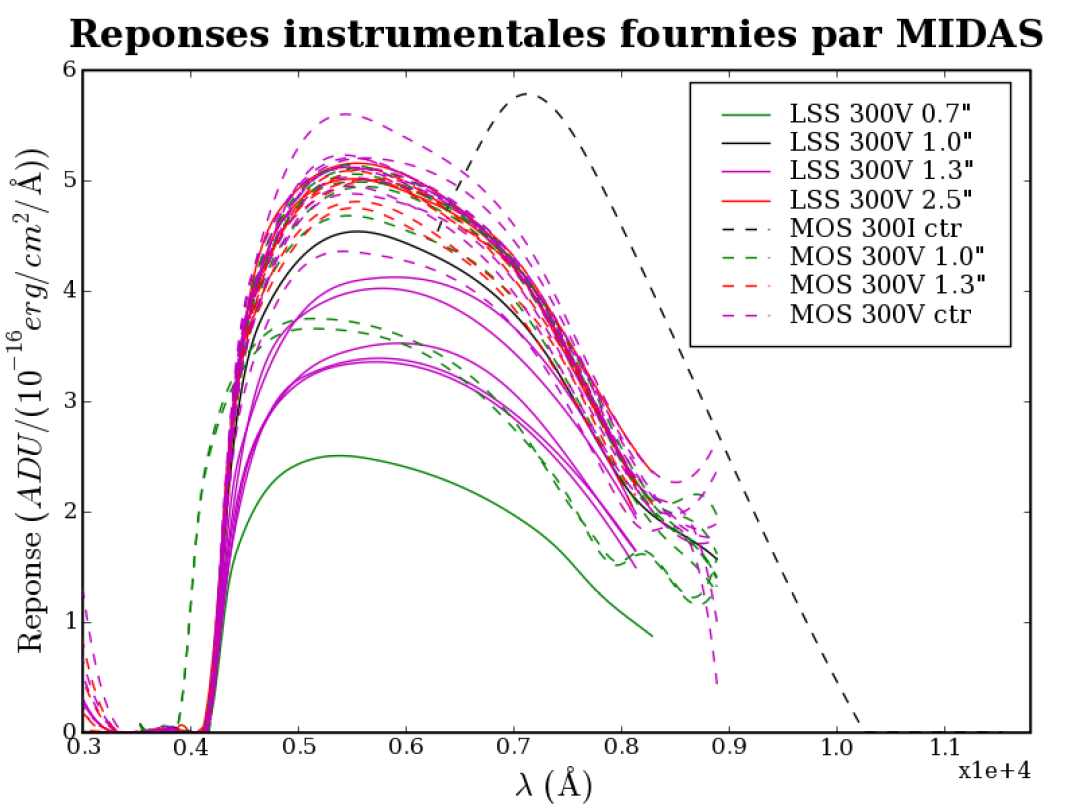
Image Pipe_Resps_UT1

Si l'on considère l'ensemble des fonctions de réponse produites par MIDAS pour FORS1 monté sur l'UT1, on constate que le niveau de réponse global peut varier du simple au double (de 2.5 à 5.5 ADU/10$ ^{16}$ erg/Å). La pente autour de 6000Å change aussi significativement. La transparence de l'atmosphère, réduite par des cirrus d'altitude, est le seul facteur pouvant expliquer de tels écarts. Les réponses obtenues en mode MOS, avec une fente large de 5'', sont légèrement plus bleues que celle en mode LSS. En effet, la qualité d'image est moins bonne dans le bleu que dans le rouge, et les fines fentes LSS coupent donc un peu plus de flux dans le bleu que dans le rouge.

Deux fonctions de réponse, prises les 28 et 29 Novembre 2003 présentent une excursion suspecte en deça de 4000Å. Cela provient de l'utilisation d'une fonction de dispersion prise avec la fente centrée, alors que le spectrogramme de l'étoile l'est à la position de la fente d'1.0'', à -12mm. C'est le genre d'erreurs humaines et de laxisme logiciel que j'ai cherché à abolir par l'automatisation des procédures.

La Base d'étoiles spectrophotométriques :

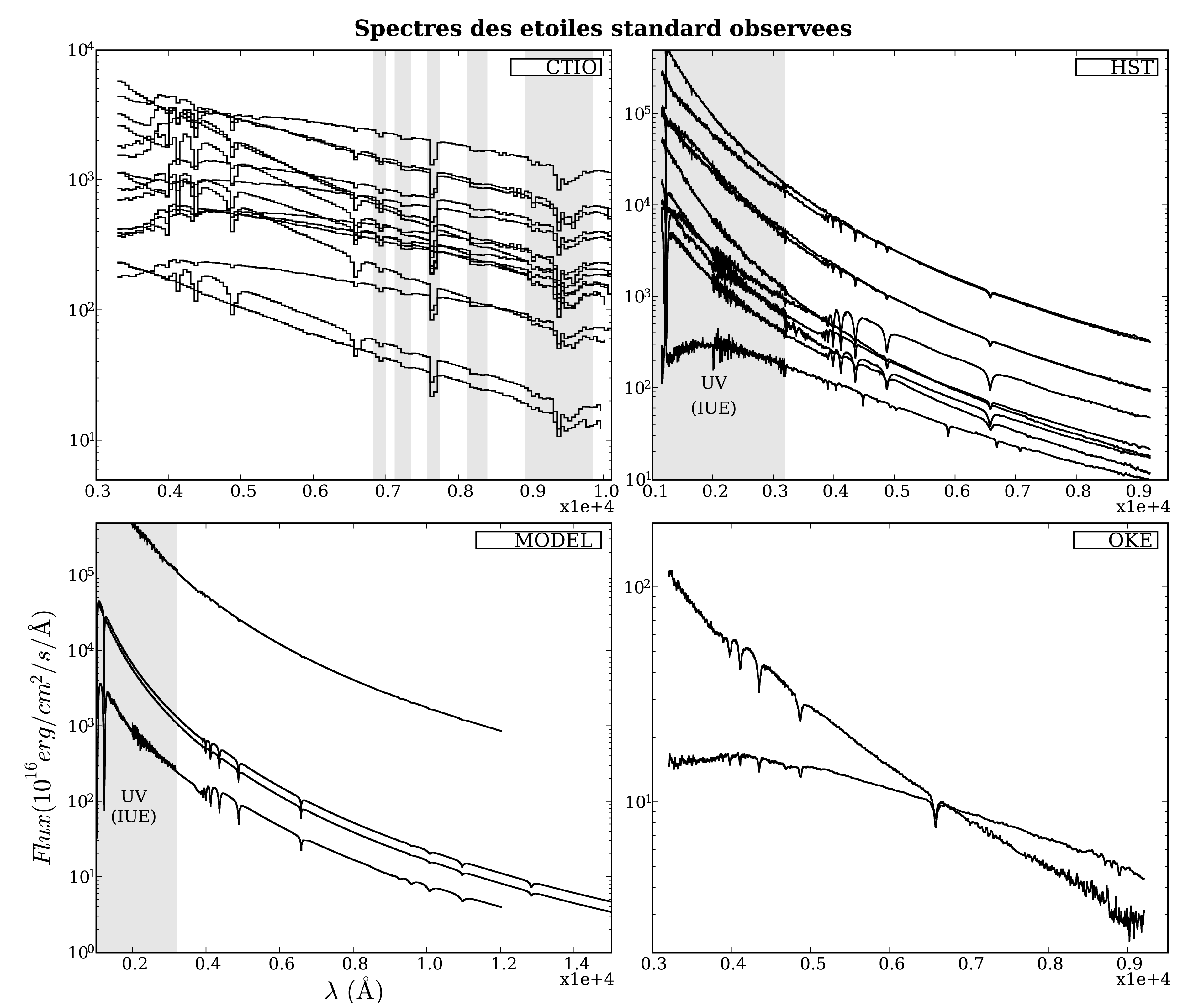
Le catalogue des spectres d'étoiles standard3.13 est composé de spectres d'étoiles chaudes et de naines blanches, de diverses provenances (CTIO, Oke, HST, modèles synthétiques de naines blanches), de diverses résolutions (de 0.7Å pour HST à 50Å pour CTIO) et de diverses couvertures en $ \lambda $ (c.f. Fig. 3.17). Certains sont corrigés de l'absorption tellurique, d'autres non (CTIO).

Figure 3.17: Spectres des étoiles de référence utilisées par l'ESO, en fonction de leur provenance, en échelle logarithmique. On remarque l'homogénéité mais la faible résolution et l'absence de correction de l'absorption tellurique des spectres CTIO. Les spectres HST ont une exellente résolution et peu de bruit au-delà de 3200Å. Les modèles de naines blanches n'ont aucun bruit, mais sont approximatifs (deux d'entre eux ne reproduisent pas les raies de l'Helium présentes dans le spectre réel). La partie UV des spectres provient du satellite IUE.

Image SpecPhot_Stds

Figure 3.18: Shéma de la nomenclature des séries de Lyman et de Balmer. Les raies d'émission correspondent au passage de l'électron d'un atome d'Hydrogène d'un niveau d'énergie E($ n_1$ = $ n_0$ +k) à un niveau E($ n_0$ ). La différence d'énergie est rayonnée via un photon de longueur d'onde $ \lambda $ . Les raies d'absorption relèvent du processus inverse. La série de Lyman correspond à $ n_0$ =1, celle de Balmer à $ n_0$ =2. Une lettre grecque sert de numérotation : la première raie de Balmer, de $ n_1$ =3 à $ n_0$ =2 sera Balmer-$ \alpha $ . Elle se trouve dans le rouge, les autres raies étant dans le bleu lointain, est donc facile à observer, très populaire, et souvent surnommée H$ \alpha $ .

\begin{picture}(150,150) \put(-5,150){{\it E(n)}} \put(100,40){(Lyman)} \par \... ... \multiput(22,148)(4,0){25}{.} \par \put(20,150){\line(1,0){100}} \end{picture}
La formule de Rydberg (1888) fournit le $ \lambda $ des transitions de l'Hydrogène : $ \frac{\Delta E}{hc} = \frac{1}{\lambda}=R_H \left( \frac{1}{n_0^2}-\frac{1}{n_1^2} \right) $ avec $ R_H$ =1.09737 10$ ^7$ m$ ^{-1}$ la constante de Rydberg.

Lyman ($ n_0$ =1) Balmer ($ n_0$ =2)
$ n_1$ nom $ \lambda (nm)$ $ n_1$ nom $ \lambda (nm)$
2 $ \alpha $ 121.568 3 $ \alpha $ 656.470
3 $ \beta $ 102.573 4 $ \beta $ 486.274
4 $ \gamma $ 97.255 5 $ \gamma $ 434.173
5 $ \delta $ 94.975 6 $ \delta $ 410.294

Plutôt que d'utiliser une fonction de réponse construite d'après l'observation d'étoile standard la plus contemporaine des observations de science, j'ai cherché à construire une unique fonction de réponse d'après l'ensemble des observations d'étoiles standard, pour chaque configuration grisme+fitre et pour chaque UT. En effet, les transmissions des filtres et l'efficacité quantique n'ont pas de raison de varier. Encore une fois, on évitera de rééchantilloner, filtrer, interpoler ou extrapoler pour rester au plus proche de la réalité. Le lissé obtenu par MIDAS en intégrant puis en interpolant sera obtenu par l'accumulation statistique d'observations, et en interpolant dans les bandes d'absorption tellurique.

Ces observations contiennent aussi l'information sur le spectre d'absorption tellurique, que l'on tentera donc d'estimer parallèlement. Comme la majorité des observations concernent des étoiles CTIO, il faut préalablement corriger leur spectre de l'absorption tellurique si l'on veut estimer celle-ci en notre site.

Une première tentative révéla que l'échelle des $ \lambda $ calibrée et celle des spectres de référence pouvaient êtres décalées de quelques Å. Ceci n'a un effet important qu'au niveau des raies d'absorption photosphériques, où la dérivée seconde du spectre devient très grande. Une correction $ dC_0$ du terme constant $ C_0$ de la fonction de dispersion, imputé à un décentrage de l'étoile standard dans la fente, se chargera de réaligner ces raies. Il faut néanmoins connaître auparavant la position, la profondeur et la largeur précise des raies de chaque spectre, pour savoir où chercher les résidus et déduire de leur amplitude le décalage local.

Caractérisation et correction des spectres de référence :

Les raies d'absorption photosphériques, reflets de la composition chimique de la ``surface lumineuse'' de l'étoile, ont un profil proche d'une fonction Lorentzienne3.14, reflet de l'agitation thermique Maxwellienne. En échelle logarithmique, le continuum dans lequel s'incrustent les raies d'absorption s'ajuste bien par un polynôme de degré 2 au-delà de 4500Å (de la congestion des raies de Balmer de l'Hydrogène, de 3700 à 4000Å), et la forme lorentzienne des raies est conservée. L'ajustement polynomial est robustifié, rejetant les raies et autres absorptions, et sert de modèle pour corriger les spectres CTIO de l'absorption tellurique. Les spectres bruités de Oke seront aussi remplacés par cet ajustement, au-delà de 6700Å(c.f. Fig. 3.19-c).

Figure 3.19: En haut : Identification et caractérisation des raies d'absorption photosphériques de l'Hydrogène de l'étoile standard LTT4816 (CTIO) (à gauche). Idem pour le modèle synthétique de la naine blanche GD 71 (à droite). En bas : Modélisation du continuum de LTT 4816 au-delà de 6700Å, corrigeant les bandes d'absorption telluriques de O2 et de H2O (à gauche). Modèles d'extinction atmosphérique au Chili (Tololo, La Silla) et à Hawaii (Gemini N). Le modèle ad-hoc utilisé, et les lois semi-empiriques de diffusion de Rayleigh (E($ \lambda $ ) $ \propto \lambda ^{-4}$ ), d'absorption de l'Ozone et des Aérosols (c.f. [7][1]) (à droite).
Image StdCaract_ltt4816 Image StdCaract_gd71
Image StdCorr_ltt4816 Image AtmoExt_Models

Ce continuum est soustrait du spectre logarithmique, ne laissant que les bosses du spectre (c.f. Fig. 3.19-a). En effet, l'ondelette n'est théoriquement pas sensible au piston (son intégrale est nulle), ni à la pente (elle est symétrique), mais les imprécisions numériques et d'échantillonnage contrarient ces propriétés. La position des raies peut donc être légèrement biaisée en présence d'un continuum incliné, et l'est définitivement par un continuum courbe.
Ce spectre plat est iterativement filtré par convolution avec une ondelette adaptée à la détection de profils de Lorentz $ L_{\Gamma_0}(\lambda)$ de largeur $ \Gamma_0$ : c'est la dérivée seconde de $ L_{\Gamma_0}(\lambda)$ , dont le produit avec $ L_{\Gamma_0}(\lambda)$ est normalisé à 1. L'à priori $ \Gamma_0$ est choisi autour de 30Å, et peut être modifié selon les cas. On estime ainsi la magnitude $ A$ des raies et leur position $ \lambda _0$ en cherchant les minimas du spectre plat filtré $ \mathcal{S}_f$ autour de la position $ \lambda _0$ attendue des raies de Balmer de HI (d'après Kurucz). La position $ \lambda _0$ et la largeur $ \Gamma_0$ sont corrigées respectivement en calculant la valeur en $ \lambda _0$ de la convolution du résidu $ \mathcal{S}_f(\lambda) - A \times L_{\Gamma_0}(\lambda-\lambda_0)$ avec la dérivée de $ L_{\Gamma_0}(\lambda)$ selon $ \lambda $ et selon $ \Gamma$ , normalisées pour que leur auto-corrélation vaille 1 en zéro (i.e. que leur carré soit unitaire : $ \int{\frac{\delta L}{\delta\Gamma}^2}d\lambda=1 $ ).

On dispose alors de nouveaux à prioris $ \lambda_1$ et $ \Gamma_1$ , et l'on itère jusqu'à ce que le critère de convergence $ \epsilon$ (i.e. $ \frac{\lambda_i-\lambda_{i-1}}{\lambda_{i-1}} < \epsilon \sim 10^{-3}$ ) soit atteint, ou que $ \Gamma_i$ devienne négatif, que $ A$ devienne positif, que l'on sorte de l'intervalle de $ \lambda $ , ou que l'on ait itéré plus de 20 fois (la solution oscille car mal contrainte). Dans les cas favorables, la convergence est atteinte en moins de 3 itérations.

Lorsque le spectre est peu résolu, la précision obtenue n'est pas fameuse. Lorsque les raies sont larges et proches, elles influent mutuellement sur leurs estimées. Mais, à quelques cas pathologiques près, traités au cas par cas, les ajustements obtenus sont satisfaisants pour les raies encore séparées au-delà de 4000Å.

Il nous faut aussi disposer d'un modèle d'extinction atmosphérique, tenant compte de la diffusion de Rayleigh sur les atomes et molécules plus petites que $ \lambda $ , de l'absorption stable de l'ozone stratosphérique et des aérosols. Divers modèles existent, pour différents observatoires, et l'on utilisera un modèle ad-hoc proche de celui CTIO, raffiné artisanalement pour que son interpolation polynomiale soit lisse (c.f. Fig. 3.19-d).

Extraction du spectre observé :

Enfin prêt à utiliser le spectrogramme, on applique à celui-ci la même procédure de calibration que celle qui servira aux spectrogrammes de science : soustraction du piédestal et division par le champ plan, estimation du fond de ciel et détection des sources. Le spectrogramme est recentré sur l'objet et réduit à la région contenant le signal ($ \lambda $ >4150Å) (c.f. Fig. 3.20). Les images de science sont en plus combinées, mais, dans le cas des étoiles standard, on ne dispose que d'une observation et cette étape est caduque. Les rares impacts de cosmiques sont détectés et retirés. Les profils intégrés dans les filtres g', r' et i' du CFHT sont calculés, et les points sources y sont détectés par un filtrage par une ondelette gaussienne adaptée au seeing attendu.

Figure 3.20: En haut : Spectrogramme MOS brut de l'étoile standard GD71. Au centre : Spectrogramme calibré du CCD, soustrait du ciel et vignété. Les couleurs des images sont en echelle logarithmique. En bas à gauche : Résultat de diverses techniques d'extraction, et spectre du ciel estimé. L'extraction d'ouverture est bruitée. L'extraction par maximum parabolique est biaisée. L'extraction par ondelette gaussienne et par ajustement de PSF gaussienne sont dépendantes du modèle de $ \sigma (\lambda )$ . L'extraction par la méthode des moments est la moins bruitée et ne dépend d'aucun modèle. On observe l'apparition du second ordre de diffraction au-delà de 8200Å. En bas à droite : Profils spatiaux intégrés dans les filtres CFHT. On observe le leger déplacement du centroïde du bleu (g') au rouge (i').
Image stdGD71_raw
Image stdGD71_master
Image stdGD71_extract Image stdGD71_extrprofs  

De ce spectrogramme intermédiaire calibré du CCD, on extrait le spectre du point source principal dans une bande d'extraction large de $ \pm $ 5$ \sigma $ , où $ \sigma $ est estimé sur le profil intégré sur toute la largeur de l'image. Trois méthodes d'extraction en aveugle sont implémentées : maximum parabolique, ondelette gaussienne et méthode des moments. La méthode des moments fournit l'estimation du flux la moins bruitée, ainsi que les estimées du centroïde selon Y et de l'étalement $ \sigma $ .
Une extraction de PSF gaussienne par minimisation de $ \chi ^2$ identique à celle qui sera utilisée pour les spectrogrammes de science combinés est aussi effectuée : le centroïde et l'étalement des profils par filtre contraignent l'inclinaison et le $ \sigma (\lambda )$ du model.
Une extraction d'ouverture pondérée par ce profil gaussien (similaire à une extraction de Horne) est aussi réalisée pour comparaison.
Le spectre extrait par la méthode des moments est corrigé de l'extinction et normalisé par le temps d'exposition et par l'intervalle de $ \lambda $ de chaque pixel.
Le spectre de référence et le spectre extrait normalisé (en ADU/s/Å) sont rééchantillonnés à un même pas (irrégulier, le plus large des deux pour intégrer au lieu d'interpoler).
L'échelle de $ \lambda $ du spectre de référence est alors corrigée pour que les raies photosphériques soient alignées avec celles du spectre extrait (c.f. Fig. 3.21).
On soustrait la participation du second ordre au-delà de 8300 Å, estimée d'après le spectre extrait. La fonction de réponse est alors calculée, et l'absorption atmosphérique dans les bandes de O2 et de H2O en est déduite. Pour cela, la fonction de réponse est interpolée par un polynôme de degré 2 dans les bandes d'absorption définies.
Enfin, le c\oeur des raies photosphériques, et les points déviants de la fonction de réponse sont filtrés par interpolation parabolique, les pertes de fente sont estimées et la réponse en est corrigée. L'estimation des pertes de fente fait l'hypothèse que le point source est centré dans la fente, et que son étalement selon X est le même que selon Y (qui est estimé en chaque X, puis ajusté par un polynôme de degré 3 ; c.f. Figure 4.9). C'est une estimation optimiste, ignorant le décentrage et le chromatisme résiduel de la réfraction atmosphérique.

Estimation du second ordre de diffraction :

Le second ordre de diffraction, si le grisme est bon, ne doit contenir qu'une faible fraction du flux incident. Cependant, pour les étoiles de référence, parfois très bleues, cette fraction $ f_{so}$ n'est pas négligeable par rapport au flux dans le rouge, et apparaît inoportunément dans la fonction de réponse. Afin de quantifier cette fraction, j'ai utilisé une observation de la naine blanche GD71, très bleue, pour tester la valeur de $ f_{so}$ . Empiriquement, $ f_{so}$ est choisie pour obtenir une fonction de réponse la plus régulière possible (c.f. Fig. 3.22). Il apparut que le facteur de doublement $ d_{so} \sim 2$ attendu entre les échelles spectrales du premier et du second ordre est en fait légèrement plus petit. Ceci peut être attribué aux aberrations chromatiques de l'étage du bas du collimateur.

Figure 3.22: À gauche : Recherche empirique de la fraction $ f_{so}$ du flux dans le second ordre. Les fonctions de réponse obtenues pour une fraction supposée allant de 1% à 5% sont tracées. La pente est conservée pour $ f_{so} \sim $ 3%, mais une difference de niveau persiste. À droite : Recherche empirique du facteur de doublement $ d_{so}$ , pour une fraction de 3%. Les ondulations disparaissent pour $ d_{so} \sim $ 1.955.
Image SecOrder_guess_frac Image SecOrder_guess_fold

On conservera les valeurs empiriques de $ f_{so}$ =0.03 et $ d_{so}$ =1.955 pour calculer les fonctions de réponse.

Construction du modèle de réponse global :

On dispose maintenant de nombreuses fonctions de réponses, dont la résolution dépend de celle du spectre de référence. Le bruit résiduel dépend fortement du bruit du spectre de référence, et de sa résolution (c.f. Fig. 3.23). Pour vérifier la consistence des diverses sources de spectres de référence, ces réponses sont combinées pour un même couple grisme+filtre, un même UT, et une même origine des références. Les modèles synthétiques approximatifs de BPM-16274 et de HD-49798 sont exclus, comme il est recommandé sur le site.

Figure 3.23: À gauche : Ensemble des 54 fonctions de réponse individuelles obtenues pour FORS1 sur l'UT1. La légende indique le mode d'observation, le grisme et la fente utilisée ou reproduite. À droite : Fonctions de réponse moyennées par grisme+filtre et par origine des spectres de référence, pour l'UT1. Le nombre de réponses individuelles moyennées est indiqué dans la légende. Le pas est de 1 Å.
Image newOff_Resps Image newOff_TmplResp

Les fonctions de réponse individuelles sont normalisées à leur valeur moyenne à 5500 Å, sur le compte de cirrus blancs. La fonction combinée est estimée avec un pas régulier de 1 Å: les interpolations paraboliques en chaque $ \lambda $ des fonctions individuelles normalisées sont moyennées. On n'observe pas de différence notable en fonction de l'origine des références, si ce n'est un niveau de bruit d'autant plus important que le pas des spectres de référence est petit et que le nombre d'observations est petit (c.f. Fig. 3.23).

Les spectres d'absorption moyens sont également combinés, et leur écart-type est calculé, renseignant sur la stabilité de l'absorption atmosphérique (c.f. Fig. 3.24-b).

Conforté sur la consistance des spectres de référence, on réitère le moyennage, cette fois sur l'origine des références. Pour aplanir les ultimes résidus et effets de bords, un filtre polynomial d'ordre 5 large de 100 Åest encore appliqué. On obtient ainsi 4 fonctions de réponse lisses et les spectres d'absorption et d'écart-type associés (c.f. Fig. 3.24). Ce distillé de références nous servira au moment de sceller toutes nos fournées de photons, en prévenant le consommateur que notre absolu de calibration, qui a été dicté par les éléments, vaut pour l'année mais pas forcément pour chaque nuit.

Figure 3.24: À gauche : Modèles finaux de la fonction de réponse, par telescope et par grisme. L'incertitude statistique propagée et l'écart-type des réponses individuelle autour du modèle, magnifiées, sont tracées pour la réponse sur l'UT2 avec le grisme 300V. Un modèle de réponse issu de MIDAS est tracé en pointillés pour comparaison. À droite : Exemple des modèle d'absorption (<0) et d'écart-type (>0) obtenus pour l'UT2 en 300V, pour le dioxygène (O2) et la vapeur d'eau (H2O), exprimés en magnitudes absorbées. La vapeur d'eau a un écart-type de même amplitude que sa moyenne, ce qui dénote des fluctuation importantes. Le dioxygène est plus stable.
Image newOff_MasterResp Image Off_Atmo

L'incertitude statistique propagée ainsi que l'écart-type des fonctions de réponse individuelles normalisées autour du modèle moyen sont bien sûr calculés. En raison du grand nombre d'observations moyennées, l'incertitude statistique est négligeable (même dans les bandes d'absorption où elle est augmentée à la louche). Le spectre de l'écart-type donne une indication de la qualité des corrections de l'extinction atmosphérique et des pertes de fentes : de la stabilité en couleur des fonctions de réponse individuelles. Comme les réponses sont normalisées à un même niveau à 5500$ \pm $ 50 Å, l'écart-type y est minimal ($ \sim $ 0.2 %).

.

On aura noté la différence de normalisation entre les réponses calculées par MIDAS, qui atteignent $ \sim $ 5 ADU/(10$ ^{16}$ erg/cm2/Å) et nos modèles qui atteignent $ \sim $ 2 ADU/(10$ ^{16}$ erg/cm2). Cela provient de la normalisation par l'intervalle de $ \lambda $ couvert par les pixels, de l'ordre de 2.65 Å, qui fournit une fonction de réponse en ADU/(erg/cm2) plutôt qu'en ADU/(erg/cm2/Å). Comme MIDAS rééchantillonne avec un pas constant en $ \lambda $ les spectrogrammes pour corriger la distorsion, ce facteur constant est inclu dans la réponse. Elle est valide pour des pixels de 2.65 Å.

Ce long détour dans l'univers des références de calibration nous a permis de modéliser à la fois la réponse de l'instrument et la transparence de l'atmosphère. Comme la majorité des observations d'étoiles standards sont effectuées en mode MOS, les étapes de calibration du CCD, de soustraction du ciel et de vignettage ont été implémentées de manière à supporter les deux modes LSS et MOS. Ainsi, ce sont les mêmes algorithmes qui sont utilisés dans les deux cas. Simplement, le mode LSS est traité comme un cas particulier du mode MOS, où il n'y a qu'une seule ouverture, couvrant tout le champ. C'est la seule ouverture qui nécessite, et qui permette d'estimer, les coefficients transversaux $ C_{y^2}$ et $ C_{xy^2}$ . Les piédestaux y sont indifférents, mais les champ-plans et les spectrogrammes de lampes à arc sont traités similairement en mode MOS (N<19 fonctions de dispersion, N=3 pour les STD 2048x400) et en mode LSS (N=1 fonction de dispersion). Les 9 bandes utilisées en mode LSS sont remplacées par deux bandes par ouverture en mode MOS.

3.4.5 Combiner : le coeur du problème.

Revenons à présent à des choses plus terre-à-terre : comment l'on résume 2 à 5 spectrogrammes de science, 2 images et 2 fonctions de calibration à un unique spectrogramme ne contenant plus que le signal des sources astrophysiques.

Le cahier des charges de l'opération demande :

$ \bullet$
de calibrer du CCD,
$ \bullet$
de soustraire le spectre du ciel (uniforme spatialement),
$ \bullet$
de vignetter les spectrogrammes à la fenêtre contenant le signal,
$ \bullet$
de combiner les $ N_{acq}$ spectrogrammes de science et
$ \bullet$
de calculer l'image du bruit propagé.

Après avoir lu la carte listant les fichiers de science et de calibration à utiliser, l'uniformité des configurations est vérifiée et le fichier FITS de sortie est initialisé. Le niveau des bords masqués est calculé, et servira à normaliser le modèle de piédestal à ce niveau. Les décalages théoriques entre les images sont calculés, en pixels, d'après les coordonnées et l'angle polaire référencés dans les en-têtes des images de science. Ils sont arrondis à l'entier le plus proche, pour pouvoir superposer les pixels centre à centre.

Projection :

Une fois ces préparatifs terminés, on va chercher à estimer le spectre du ciel de chaque image. Comme on ne sait pas à priori où se trouvent les sources, qui doivent être exclues de l'estimation du ciel, une première estimation est faite dans 16 bandes horizontales : pour chaque colonne d'une bande, les pixels sont corrigés du piédestal normalisé et du champ-plan. L'algorithme de moyenne robuste, avec une exclusion haute à 5$ \sigma $ , fournit l'estimée du niveau du ciel dans cette bande, mais surtout la trace des pixels ayant été rejetés (valant 0 ou 1). On additionne ces traces de réjection pour toutes les colonnes pour obtenir la trace de réjection selon Y de chaque image.
Tenant compte des décalages entre images, et avec une fraction minimale de réjection sur une ligne entière donnée (de 5% pour les images de science, de 20 % pour les étoiles standard), on masque les lignes soupçonnées de contenir plus que du ciel. La position $ Y_s$ de la source principale est calculée, pour peu qu'il y en ait une (sinon, le centre de l'image est utilisé, c.f. Fig. 3.25).
La raie de [OI] ionosphérique à 5577.34 Å est identifiée sur les spectres de chaque région, et sert à corriger la flexion et la torsion de l'instrument via $ C_0$ et $ C_y$ .
Ceci fait, on redéfinit les bandes dans une fenêtre de 400 pixels autour de $ Y_s$ , en évitant les sources masquées, pour chaque image. Si une seule source est détectée (plusieures lignes contiguës masquées), on obtient deux bandes de 200 pixels (moins la demi-largeur de la source plus 5 pixels de marge).
Le spectre du ciel est alors réestimé dans ces bandes adjacentes à la source, transposé dans l'espace spectral et interpolé cubiquement puis moyenné en suréchantillonnant à 0.2 Å, et en pondérant par la taille de la bande (c.f. Fig. 3.25).

Figure 3.25: À gauche : Exemple de traces de réjection, dans le cas d'une cible trop faible pour être décelé à 5$ \sigma $ (04D4it). Une étoile de champ voisine (à Y=590 sur la première image) serait en revanche décelée à 10% par l'algorithme, si elle se trouvait dans la fenêtre de sortie. À droite : Illustration sur la raie de [OI] de l'interpolation cubique du spectre du ciel estimé dans deux régions. Le modèle est la moyenne des polynômes de degré 3 passant par les 4 points autour des $ \lambda $ d'échantillonnage. Ici, les bandes, symétriques par rapport à $ Y_s \sim Y_0$ , n'ont pas de décalage en $ \lambda $ .
Image Reject_Trace Image Sky_Interpol

Combinazion (in italiano) :

Il est simple maintenant de combiner les images de science : On définit la fenêtre d'intérêt pour qu'elle couvre l'intervalle de $ \lambda $ du filtre utilisé, et qu'elle soit large de 2$ N_{y}$ =200 pixels autour de la source principale. Pour chaque pixel de la fenêtre de sortie, les $ N_{acq}$ pixels correspondant des $ N_{acq}$ images de science sont calibrés par leur piédestal et champ-plan respectifs, les valeurs du modèle moyen de ciel en $ \lambda({\tt X},{\tt Y})$ en sont soustraites, leurs incertidudes sont calculées, et l'algorithme de moyenne robuste à $ \pm $ 5$ \sigma $ leur est appliqué. On obtient ainsi la valeur moyenne en ce pixel de sortie, ainsi que son incertitude propagée (c.f. Fig. 3.26, pour une supernovæ parmi les plus lointaine, très faible).

On s'abstient à ce stade d'appliquer la fonction de réponse, qui le sera sur les spectres extraits, mais elle est copiée dans une table en extension pour être disponible par la suite.

Figure 3.26: Images : (haut) : Centre du quatrième des 5 spectrogrammes bruts de SN-04D4it (possible SN-I à z $ \sim $ 1, $ M_{r'} \sim $ 24, autour du maximum). (centre) : Spectrogramme combiné et soustrait du ciel. (bas) : Image du bruit propagé, contenant le bruit de lecture et le bruit du ciel, affectés par le champ plan. Graphiques : (a) : Modèle du spectre du ciel de la première acquisition en echelle log. (b) : Histogramme log du spectrogramme combiné, et ajustement gaussien. (c) : Carte des 1473 (0.8 $ \%_0$ ) impacts de cosmiques trouvés (+) et des 5 résidus filtrés ($ \circ $ ). (d) : Histogramme de puissance log-log des rayons cosmiques trouvés.
SN-04D4it, 5$ \times $ 750 sec., 300V, 1.0''. Le 20/09/2004 (MMJD=629.082 jours).
Image 04D4it_raw4
Image 04D4it_comb5
Image 04D4it_noise
Image Sky_Model Image Comb_Histo
Image Reject_Map Image Cosmic_Histo

Le filtrage temporel fonctionne tant qu'il y a moins de pixels impactés que non-impactés. Il arrive parfois que 3 images sur 5 soient impactées aux mêmes coordonnées, auxquel cas ce sont les pixels justes qui sont rejetés. On détecte ces rares pixels malchanceux par leur excursion au dessus du niveau moyen périphérique, au moyen d'ondelettes bidimensionnelles. Ils prennent la valeur du contour, et leur bruit se voit augmenté de leur excursion.

Les en-têtes aussi sont propagés (en partie, et en simplifiant le nom des clefs), actualisés si nécessaire, et complétés avec les paramètres utilisés. La première image sert de référence de coordonées et de fonction de dispersion au produit combiné. Les étapes les plus lentes sont l'estimation du ciel sur toute l'image, puis dans les bandes contiguës, puis le moyennage des images. L'implémentation fait un compromis entre la taille des vecteurs intermédiaires remplis et le nombre d'accès requis aux fichiers. Les paramètres fournis ici sont les valeurs par défaut, mais ils sont modifiables optionnellement par la ligne de commande. Ainsi, si l'on veut combiner les images entières, il suffit de préciser $ N_{y}$ =1000 dans la ligne de commande (-y 1000).

Les coordonnées et le flux des pixels rejetés lors du moyennage sont conservés dans une table en extension, de même que pour ceux filtrés ensuite sur l'image combinée.

Pondération :

La qualité d'image -le piqué- de chaque acquisition dépend du seeing sur la ligne de visée au cours de l'acquisition. Censément, on aimerait donner plus de poids aux images les plus piquées. Les observatoires disposent souvent d'un DIMM, qui mesure la stabilité atmosphérique en observant le mouvement relatif des images d'une étoile brillante à travers deux pupilles proches3.15. Le seeing qui en est dérivé au début et à la fin de chaque pose est enregistré dans l'en-tête de l'image, si le DIMM fonctionne (sinon il vaut -1).

On peut utiliser leur moyenne pour pondérer les images, mais cela suppose que le seeing varie lentement au cours des 10 minutes de la pose, ce qui est loin d'être acquis. D'autre part, la ligne de visée du DIMM ne correspond pas à celle de l'UT. En insistant auprès des astronomes de Paranal, j'ai obtenu un DVD des archives d'observation de nos nuits (en fait, de toutes les nuits de 2003-2004). On y trouve le seeing du DIMM à chaque minute, mais surtout l'objet de mon désir : l'étalement de l'étoile de guidage, calculé toutes les 30 secondes afin de corriger la forme du miroir primaire pendant sa course (l'optique active). Ces valeurs sont théoriquement plus adaptées à nos observations : toujours disponibles car les UTs n'observent pas sans guidage ni optique active, et prises parfaitement sur notre ligne de visée.

On utilise donc le seeing synthétique -moyen3.16- calculé d'après ces valeurs pour pondérer chaque image. Pour donner plus de poids aux seeings les plus faibles, on pondère par 1/seeing$ ^4$ .

En fait, ce serait trop simple, ces valeurs restent parfois bizarrement bloquées plus ou moins longtemps à une valeur précise (c.f Fig. 3.27). L'ESO connaît et étudie ce problème logiciel, et l'on s'en accommode en espérant que les valeurs soient tout de même qualitativement valables.

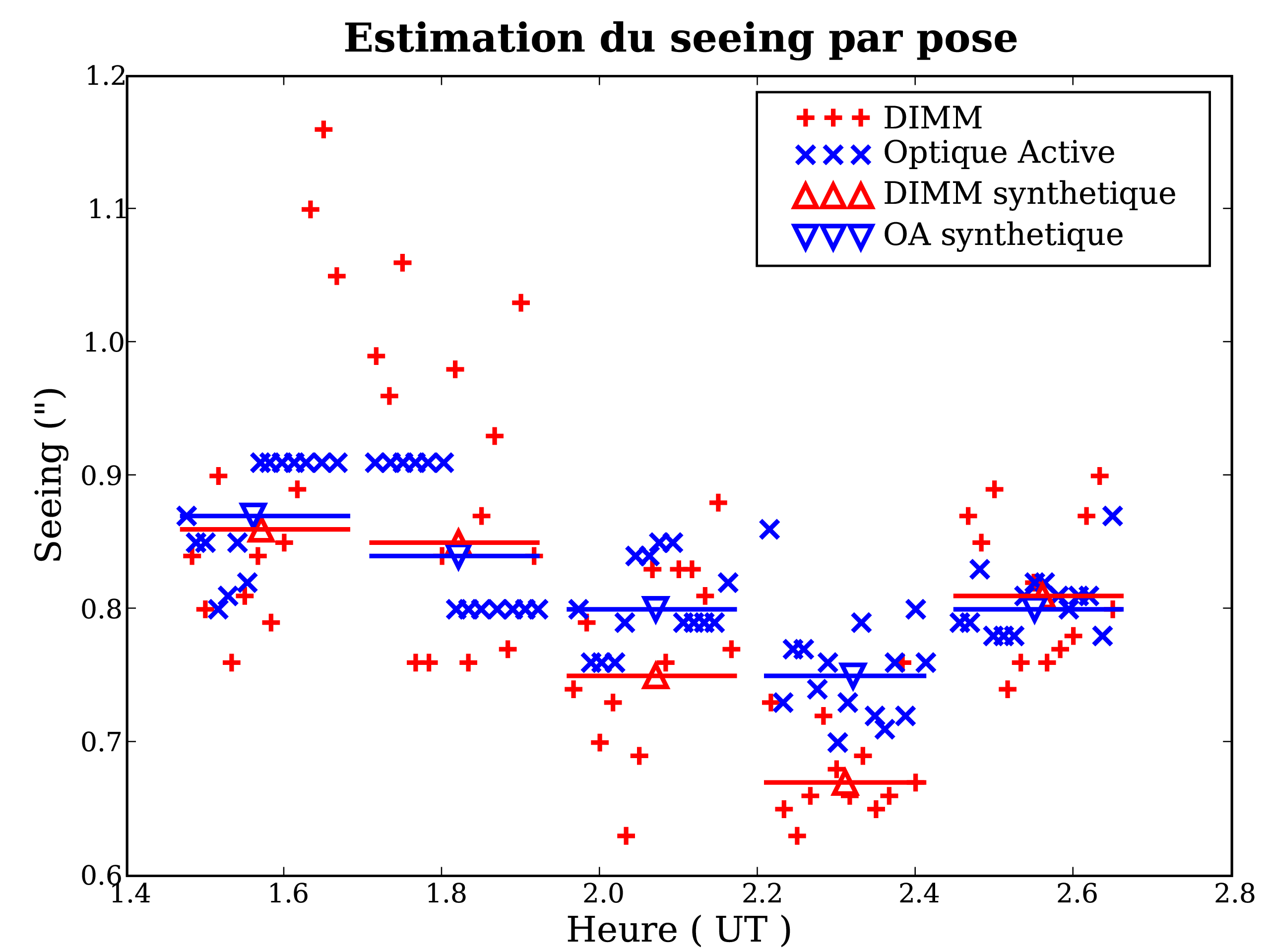Image Seeings
Figure: Seeings enregistrés par le DIMM (+) et sur l'étoile guide pour l'optique active ($ \times $ ) au cours des 5 poses de SN-04D4it. Les moyennes synthétiques par pose sont représentées par les triangles, et la durée des poses par les barres.
 

Les fluctuations du seeing peuvent aussi avoir une conséquence vicieuse : au moment de combiner les images, à l'endroit de la source, une image très piquée risque d'avoir un flux plus fort que les autres images, et d'être bêtement rejetée par l'algorithme de moyenne robuste. Un tel phénomène sera décelable sur l'image du bruit, car moins de pixels sont moyennés, donc le bruit propagé est plus élevé sur l'éventuelle crête tronquée; ou en examinant la carte des pixels rejetés. Si le signal est faible, comme c'est souvent le cas, il sera dur de dépasser le niveau de réjection. Dans les faits, ce phénomène n'a été vu qu'une fois, mais à cause d'une première image dépointée, vide, sur 6 (offerte par l'ESO).

next up previous contents
Next: 3.5 Digression sur le Up: 3. Les promesses de Previous: 3.3 Propagation des erreurs
Sylvain Baumont
2010-01-11