- ... d\'eg\'en\'er\'es1.1
-
On parle de gaz dégénéré lorsque la densité d'états quantiques
possibles est égale à la densité de particules, qui les occupent donc tous.
Une pression quantique s'oppose alors à toute contraction.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... m\'etaux1.2
-
les astronomes appellent métal tout élément plus lourd que l'Hélium :
non primordial
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... parallaxe1.3
-
qu'utilise notre cerveau pour voir en relief à partir des images
fournies par chaque oeil
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
l'ESO2.1
- http://www.eso.org/observing/etc/
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
lumineux2.2
- on parle alors de réseau blazé
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
th\`ese2.3
- Spectroscopie des supernovæ à grand décalage vers le rouge (09/2004)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... variance3.1
-
Variance ou second moment centré :
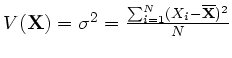 , avec
, avec
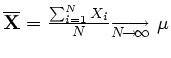 la moyenne de
la moyenne de
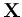 , et
, et 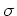 son écart-type.
son écart-type.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... interpr\'et\'e3.2
-
C++ est un language compilé : un programme est traduit en assembleur
dans un fichier directement executable par le processeur.
Python est un language interprété : un programme est executé
tel quel ligne par ligne par l'interpréteur Python, qui doit être
installé sur le poste de calcul.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...normale3.3
-
``courbe en cloche'', ou Gaussienne, de densité de probabilité
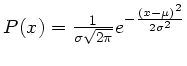 ,
pour une variable de moyenne
,
pour une variable de moyenne 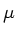 et d'écart-type
et d'écart-type 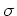 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Poissonnienne3.4
-
Loi de Répartition Poissonienne de taux
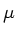 :=
:=
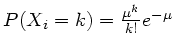 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... analyses3.5
- On ne dispose de toutes façon pas, en mode service,
des images de calibration permettant de l'estimer, très coûteuses en temps
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... gain3.6
-
La réponse instrumentale inclut le gain de conversion, et est expimée en
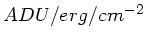
![$ \left( \mathcal{R}=\frac{AT}{f} \frac{q [e^-/h\nu]}{g [e^-/ADU]}
\quad [ADU/h\nu] \right)$](img165.png)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... lecture3.7
-
La lecture des pixels peut se faire par 1 ou 4 ports
(plus rapide, utilisé pour les pré-acquisitions de pointage),
en groupant les pixels par paires, et avec un gain haut ou bas.
Les images de science sont lues par 1 port, sans groupement, et avec le gain haut :
CLOCK = A,1x1,high.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...blanche3.8
-
i.e. indépendante de
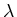 , donc du couple fente/grisme, par opposition
aux franges colorées.
, donc du couple fente/grisme, par opposition
aux franges colorées.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...crénelage3.9
- ou aliasing : apparition
de signaux artificiels à des fréquences proches de celle du
rééchantillonnage lorsque celui-ci ne respecte pas le critère de
Shannon-Nyquist d'un pas inferieur à la moitié des plus petits détails
du signal.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... FORS1+23.10
-
FORS1+2 User Manual [16] :
www.eso.org/instruments/fors/doc/VLT-MAN-ESO-13100-1543_v77.pdf
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Kurzuc3.11
-
Dans MIDAS calib (disponible à ftphost.hq.eso.org/midaspub/calib) :
sous midas/calib/data/spec/line/.
Dans IRAF (disponible à www.stecf.org/iraf/web/):
sous /iraf/noao/lib/linelists/.
Kurucz Atomic Line Database:
cfa-www.harvard.edu/amdata/ampdata/kurucz23/sekur.html
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...lapack3.12
- Linear Algrebra PACKage :
www.netlib.org/lapack/
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... standard3.13
- disponible à
www.eso.org/observing/standards/spectra/
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
Lorentzienne3.14
-
fonction Lorentzienne centrée de largeur à mi-hauteur
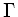 :
:
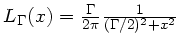
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
proches3.15
- voir le site des conditions météorologiques de Paranal :
http://archive.eso.org/asm/ambient-server?site=paranal.
Voir [15] pour une étude statistique des couches turbulences au dessus
du Cerro Tololo.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... -moyen3.16
- L'écart-type
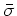 de la somme des gaussiennes centrées d'écart-type
de la somme des gaussiennes centrées d'écart-type 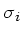
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... TERAPIX4.1
- Traitement Élementaire,
Réduction et Analyse des PIXels de megacam.
Voir http://terapix.iap.fr/
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (1941)4.2
-
Local structure of turbulence in incompressible fluid for very high Reynolds
numbers.
AN Kolmogorov - Dokl. Akad. Nauk SSSR, 1941
Traduction : RSPSA vol. 434, no. 1890, July 8, 1991, p. 9-13
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
atmosph\'erique4.3
- Le chromatisme de la réfration atmosphérique, à
l'origine de phénomènes tels que le rayon vert
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... l'observation4.4
- calculée comme
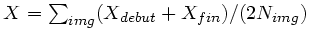 , avec
, avec 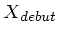 et
et
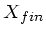 pris dans les en-têtes : TEL AIRM START et END.
pris dans les en-têtes : TEL AIRM START et END.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
\'equivalente4.5
- La largeur qu'aurait la raie si elle absorbait tout le flux
dans un intervalle de
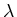 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... exemple5.2
-
la base du logarithme ainsi que
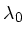 sont choisis arbitrairement à 10
et 5000 Å
sont choisis arbitrairement à 10
et 5000 Å
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
l'exponentielle5.3
-
ceci afin d'éviter d'avoir une normalisation négative
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
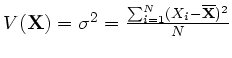 , avec
, avec
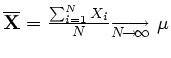 la moyenne de
la moyenne de
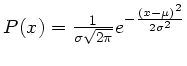 ,
pour une variable de moyenne
,
pour une variable de moyenne 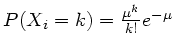 .
.
![$ \left( \mathcal{R}=\frac{AT}{f} \frac{q [e^-/h\nu]}{g [e^-/ADU]}
\quad [ADU/h\nu] \right)$](img165.png)