4.4 Les touches finales

L'extraction des ADUs correspond au gros $\oe$ uvre, posant les bases des spectres finaux. Une fois satisfait de ces bases, il convient de les calibrer, de vérifier la validité des hypothèses faites, et de finaliser le conditionnement des produits finaux.

4.4.1 Normalisation et Calibration

La calibration est destinée à exprimer les flux estimés en unités physiques standard (erg/s/m $^2/\AA$ ), via la fonction de réponse.

Ensuite, la normalisation consiste à corriger ce flux de l'effet des agents intervenants : l'extinction atmosphérique, l'absorption tellurique et les pertes de fente. L'extinction est tabulée, l'absorption a été estimée lors du calcul de la réponse, et les pertes de fente sont calculées d'après le seeing, $\kappa$ , et la largeur de la fente.

La réponse instrumentale :

J'ai détaillé dans la section 3.4 comment une unique fonction de réponse a été construite pour chaque couple grisme+filtre et pour chaque télescope d'après les observations d'étoiles standard. Elles sont utilisées ici, telles quelles, et tant qu'elles dépassent 10 $^{-3}$ ADU/(10 $^{-16}$ erg/cm

Chaque spectre extrait est divisé par le temps d'exposition et par l'intervalle de $\lambda$ des pixels, puis par la fonction de réponse. Le même traitement est appliqué aux spectres du bruit propagé.

L'extinction atmosphérique :

L'extinction atmosphérique est calculée avec le même modèle que celui utilisé pour corriger les spectres d'étoile standard. Ceci est important, car la fonction de réponse a été calculée pour cette fonction d'extinction. Une fonction d'extinction différente aboutirait à une fonction de réponse différente. Elles vont donc de paire.

L'extinction $E(\lambda)$ est exprimée en magnitudes absorbées, pour une masse d'air unitaire (observation au zénith). Le flux est donc multiplié par 10 $^{X E(\lambda)/2.5}$ ,

étant la masse d'air moyenne de l'observation^4.4.

L'absorption tellurique :

On a aussi vu en section 3.4 que le spectre d'absorption par les molécules de vapeur d'eau et de dioxygène est très variable, en particulier pour la vapeur d'eau.

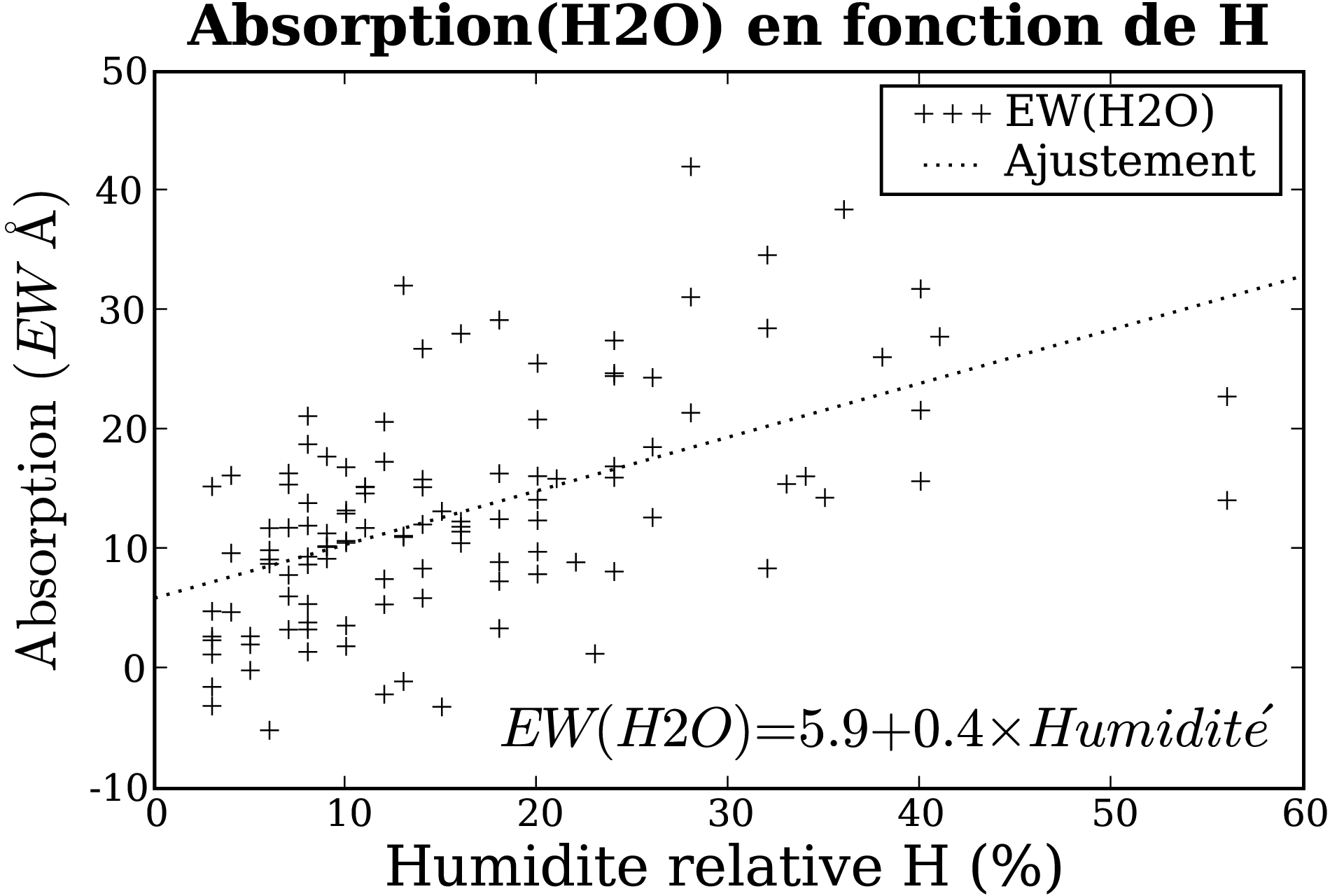
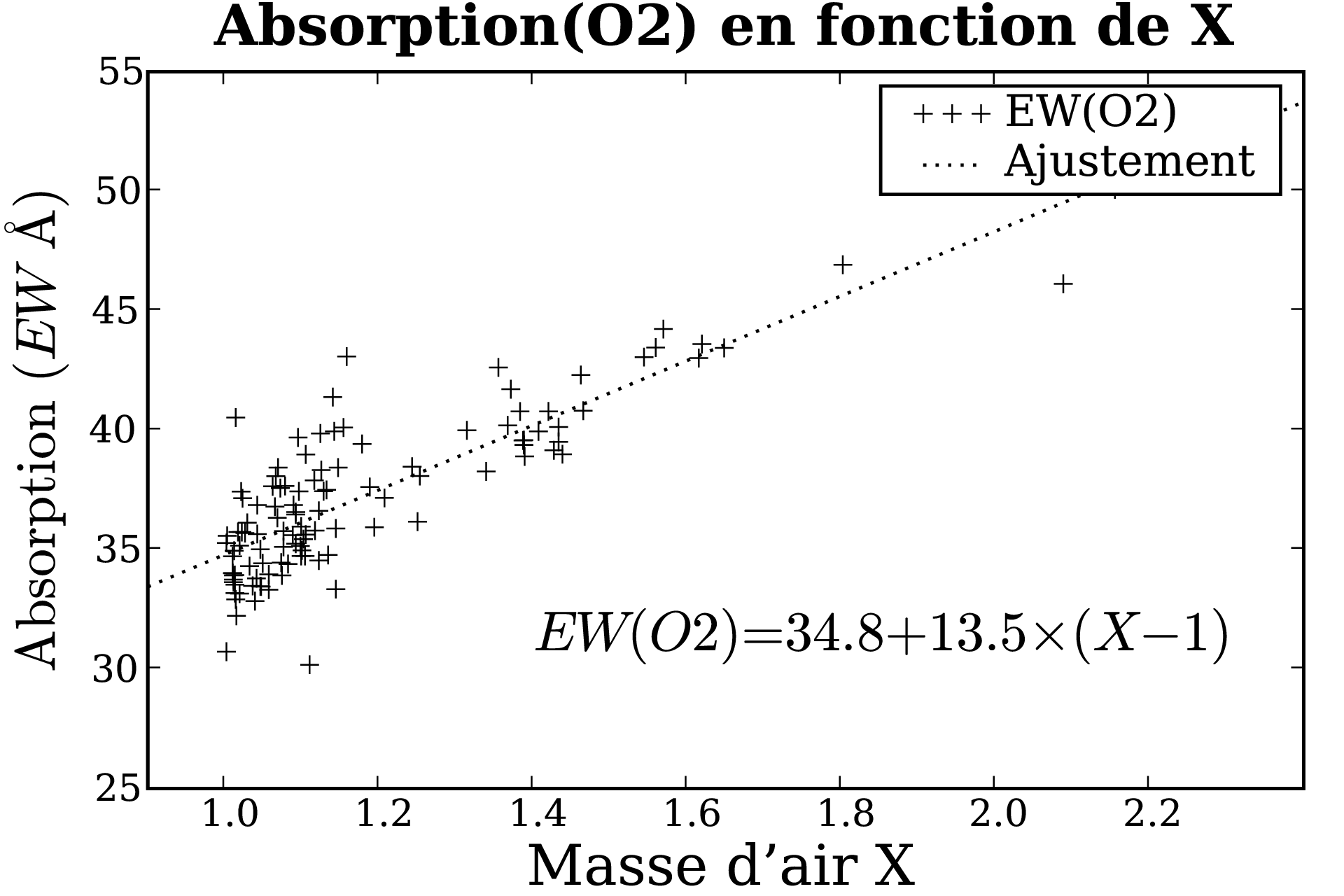
Pour chercher d'eventuelles corrélations permettant d'anticiper ces fluctuations, on définit l'intensité d'absorption par chaque molécule comme la largeur équivalente^4.5 du spectre d'absorption dans les bandes propres à la molécule, pour chaque spectre de référence. Cette intensité est tracée en fonction des conditions ambiantes de l'observation conservées dans les en-têtes (température, pression, humidité). Le bon sens s'attend à une corrélation entre l'intensité d'absorption de la vapeur d'eau et l'humidité ambiante mesurée par la station météo du Cerro Paranal.

**Figure 4.15:** **À gauche :** Largeur équivalente (EW) d'absorption par H2O, en fonction de l'humidité relative ambiante lue dans les en-têtes des spectrogrammes d'étoiles standard. **À droite :** Largeur équivalente d'absorption par O2, en fonction de la masse d'air lue dans les en-têtes des spectrogrammes d'étoiles standard.

En fait, une telle corrélation n'apparaît que de manière marginale (c.f. Fig. 4.15), car la station mesure l'humidité au sol, alors que le spectre subit celle de toutes les couches atmosphériques traversées.

La seule autre corrélation visible lie l'absorption par O2 et la masse d'air de l'observation. Comme la masse d'air des observations de science est imposée à moins de 1.4, et que la dispersion autour de l'ajustement dans cet intervalle est du même ordre que l'excursion de l'ajustement (5.4 Å), on préfère utiliser un spectre d'absorption unique pour toutes les observations. On procède de même pour H2O.

Cela permet de corriger la majeur partie de l'absorption, avec une hypothèse simple (et simpliste), facilement réversible.

Les pertes de fente :

Contrairement à ce qui est fait lors du calcul des fonctions de réponse, les pertes de fentes sont estimées, non pas à partir du spectrogramme, mais à partir du seeing effectif estimé, en supposant une PSF gaussienne centrée dans la fente et un indice $\kappa$ =-0.2.

À chaque $\lambda$ , la fraction $f_{perte}$ du flux bloqué par la fente par rapport à celle transmise est calculée numériquement. Le spectre est alors multiplié par 1+ $f_{perte}$ pour lui rendre le flux bloqué.

**Figure 4.16:** Fonctions de calibration en flux utilisées pour 04D4it, avec =1.034, un *seeing* de 0.83'' en et une fente de 1''. Les fonctions d'extinction, d'absorption et de pertes sont exprimées en magnitudes absorbées. La largeur du trait des fonctions de réponse et d'absorption materialisent l'écart-type estimé.

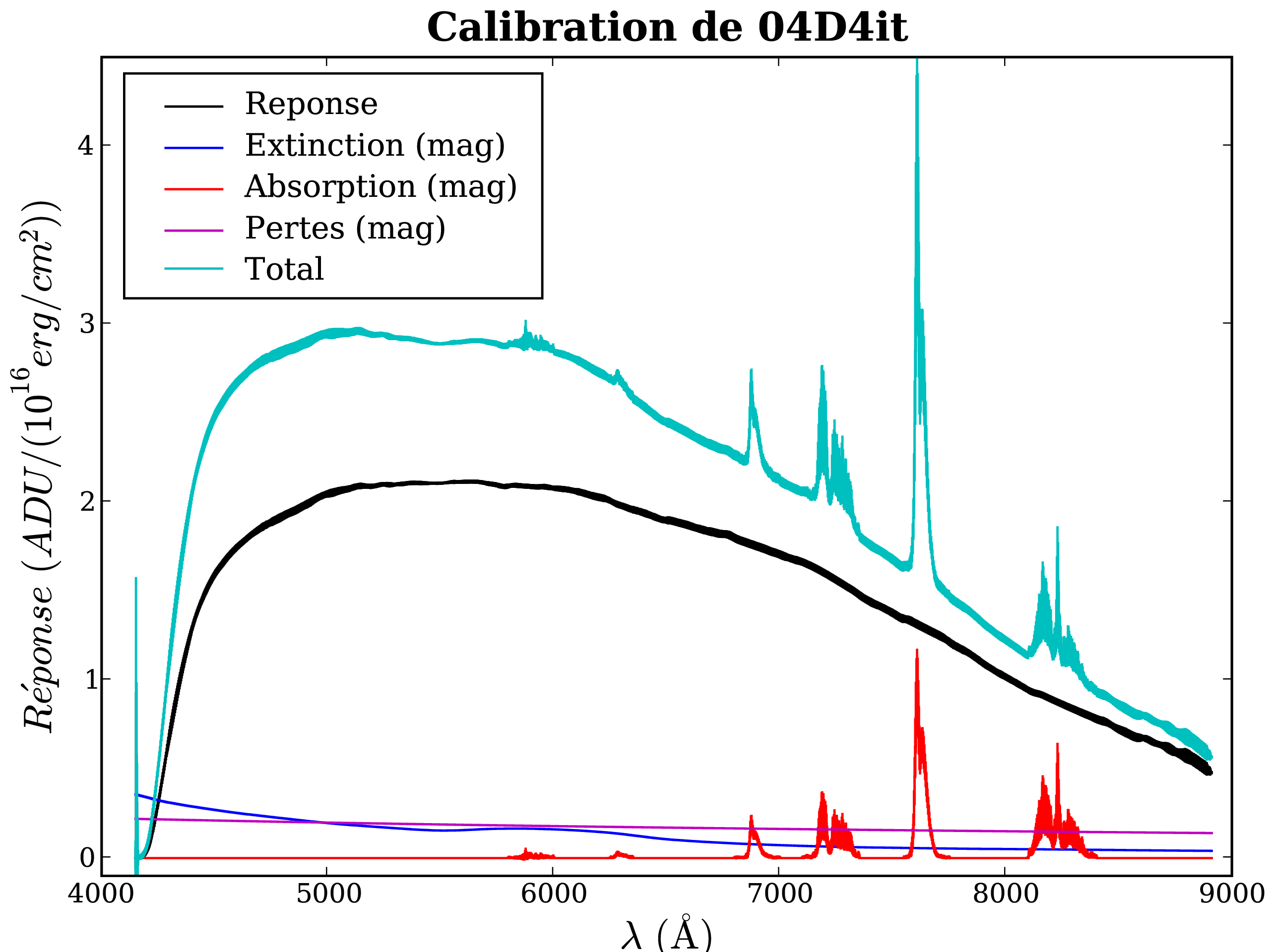L'ensemble de ces fonctions de calibration et de normalisation sont conservées dans l'extension CALIBS du spectrogramme résiduel. Leur contributions respectives sont présentées en figure 4.16, ainsi que la normalisation totale, effective, pour la supernova 04D4it.

4.4.2 Pondérations et Masques

Au cours des multiples étapes aboutissant au spectre extrait, nombre de quantités intermédiaires sont estimées, tels le spectre du ciel, les profils intégrés ou le spectre d'absorption tellurique. Que l'estimation soit obtenue par moyenne simple, robuste, ou par minimisation du $\chi ^2$ , une pondération est systématiquement appliquée, pour donner moins de poids aux données les plus incertaines.

Si l'on dispose d'une estimation de l'écart-type $\sigma_i$ des données, ce qui est le cas pour les variables internes, on démontre qu'une pondération par $\omega_i = 1/\sigma_i^2$ fournit le plus faible écart-type du résultat, à condition que l'écart-type soit bien estimé. C'est la pondération généralement utilisée, sauf pour le modèle de spectre du ciel (les spectres par région sont pondérés par la hauteur de la région et inversement à leur distance du centre

), et pour l'ajustement des résidus (pondération par le rapport du flux extrait sur le bruit propagé).

L'incertitude du résultat est calculée comme la somme quadratique des incertitudes individuelles, également pondérées, lorsqu'il s'agit d'une moyenne (avec l'hypothèse d'événements indépendants). Dans la cas de la minimisation du $\chi ^2$ , les poids $\omega_i$ sont introduits dans le $\chi ^2$ . Par exemple, l'ajustement selon

de données

par un modèle linéaire à deux paramètres $\mathcal{M}(\alpha, \beta, x)=\alpha \mathcal{A}(x) + \beta \mathcal{B}(x)$ s'écrit :

$\displaystyle \chi^2 = \sum_i \omega_i [ D_i - \mathcal{M}(\alpha,\beta, x_i) ]^2$

$\displaystyle \hspace{-0.5cm} \frac{\partial \chi^2}{\partial \alpha} = \frac{... ...thcal{A}(x_i) D_i \\ \sum_i \omega_i \mathcal{B}(x_i) D_i \end{array} \right]$

La matrice de gauche est appelée la matrice des poids, et son inverse correspond à la matrice des variances-covariances des paramètres calculés $\alpha$ et $\beta$ . On dispose ainsi d'une incertitude associée aux paramètres estimés, qui servira par la suite à pondérer une nouvelle estimation ou à définir un critère de convergence.

Cas des points aberrants :

Malgré le soin apporté au traitement des données, il arrive qu'un flux soit négatif, ou incroyablement élevé. Les bords des images, les impuretés profondes dont la transparence est surestimée par le champ plan

à cause des fuites de charges provenant des pixels contigus bien illuminés, sont des lieux privilégiés de telles aberrations.

Avec des rustines adaptées (i.e. un test que

>0.01), ces points se voient simplement affectés un poids nul, qui annulera leur contribution à l'estimée. En pratique, on essaye de limiter les aberrations au plus tôt dans la chaîne de réduction (i.e. forcer à 1 les valeurs négatives des champs plans).

Pour invalider cette colonne ainsi que celles pour lesquelles la fonction de réponse est trop basse ( $\mathcal{R}$ <0.005) ou l'absorption tellurique trop forte ( $\mathcal{A}$ >1 mag), un masque accompagne le spectre extrait. Il vaut 0 lorsque le point de mesure est fiable, et 1 lorsqu'il est déconseillé de l'utiliser. C'est un complément utile aux autres spectres de contrôle enregistrés, car il les résume succintement pour les utilisateurs peu désireux de remonter aux sources des incertitudes.

4.4.3 Contrôle de consistence photométrique

Dès lors que l'on dispose des spectres des objets, il est possible de verifier leur cohérence avec le modèle photométrique : que les spectres des galaxies, intégrés dans les filtres photométriques de MégaCam, aboutissent aux mêmes flux que sur les images de référence, et que celui de la supernova s'accorde avec sa courbe de lumière.

Il faut pour cela savoir exprimer ces flux dans les mêmes unités. La magnitude dite AB d'un objet, relative à un filtre de réponse $T(\lambda)$ donné, est calculée directement à partir de son spectre exprimé en unités SI (en erg/s/cm

), intégré dans ce filtre :

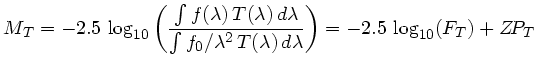
$\displaystyle M_T = -2.5 \log_{10}\left( \frac{\int f(\lambda) T(\lambda) d\... ...nt f_0/\lambda^2 T(\lambda) d\lambda} \right) = -2.5 \log_{10}(F_T)+Z\!P_T$

Ce calcul peut être fait dans touts les filtres couverts par les spectres extraits, puis être comparé aux magnitudes $\hat{M}_T$ déduites des images de référence dans chaque filtre, moyennant la valeur du point zéro de MégaCam pour ce filtre :

La qualité de l'extraction peut être adréssée en absolu : retrouve-t-on tout le flux de l'objet, comme en relatif : retrouve-t-on les mêmes couleurs? On définit ainsi $\Delta M$ comme la différence des magnitudes $M_{r'}$ et $\hat{M}_{r'}$ relatives au filtre central (soit

pour les observation prises avec le grisme 300V ;

en 300I), et $\sigma M$ comme l'écart-type des différences de magnitudes dans les autres filtres, relativement à $\Delta M$ :

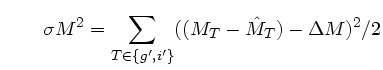
et $\displaystyle \quad\quad \sigma M^2 = \sum_{T \in \{g',i'\}}( (M_{T} - \hat{M}_{T})-\Delta M )^2/2$

Pour la supernova, le flux au moment de l'observation spectroscopique ne peut être estimé qu'à partir les courbes de lumière, de la même manière que lors de la procédure d'adéquation spectro-photométrique (section 4.1.1), et avec les mêmes réserves (la précision est sujette à la densité d'observation photométrique autour de la date d'observation spectroscopique). De même, ce flux est convertit en magnitude AB par l'intermédiaire d'un point zéro de calibration.

Lorsque la supernova et sa galaxie hôte sont extraites conjointement, leurs flux réspectifs sont additionnés pour estimer la magnitude de la composante SNGAL.

Au vu de la variabilité de la fonction de réponse (c.f. Figure 3.23) on doit s'attendre à une certaine incompatibilité des flux en valeur absolue. En revanche, la spectroscopie ayant pour but de mesurer la distribution spectrale de puissance, il est souhaitable que l'extraction respecte les couleurs des objets. Ces couleurs sont en effet déterminantes pour la classification des supernovæ ainsi que pour celle des galaxies.

Figure 4.17: Graphiques et spectrogrammes résumant la procédure d'extraction dédiée appliquée à la mascotte 03D4ag. Ces produits de contrôle sont crées et rassemblés automatiquement dans des pages en ligne pour chaque observation.



Spectrogramme combiné


Spectrogramme résiduel

On constate que les flux extraits sont plus élevés que les flux attendus, de 0.2 magnitude en moyenne (soit d'environ 20%). Cet écart peut être interprété comme la conséquence d'une fonction de réponse sous-estimée, ou d'une imprécision des points zéros. Concernant le flux de la supernova, il apparaît ici que le manque de points de mesures photométriques à proximité de la date de spectroscopie (mise à part pour la bande

) est la principale source d'imprécision. En effet, l'accroissement rapide de la luminosité de la supernova avant le maximum n'est pas bien reproduit par l'interpolation linéaire (en

en particulier). Les valeurs de $\Delta M$ et de $\sigma M$ en sont affectées. L'utilisation du modèle SALT2 pour prédire le flux à une date donnée est souhaitable, à condition d'avoir acquis la certitude que le candidat est une supernova de type Ia.

Le spectrogramme des résidus montre que la PSF est plus piquée qu'une gaussienne (à la position de la supernova), une courbure de la trace vers le bas dans le bleu ainsi qu'une imperfection du modèle des bras dans le bleu (où ils sont plus éloignés du c $\oe$ ur).

Néanmoins, les spectres du c $\oe$ ur et de la supernova ne montrent quasiment aucune contamination par les raies d'emission des bras spiraux, validant le bon comportement de l'algorithme d'extraction des sources dans ce cas d'école (galaxie résolue vue de face).