next up previous contents
Next: 4.4 Les touches finales Up: 4. Jouer toutes ses Previous: 4.2 Limites de la

Sous-sections


4.3 Utilisation des résidus

Disposant des spectres estimés d'après les à prioris, il est possible de soustraire le modèle bidimensionnel correspondant du spectrogramme combiné. On obtient ainsi le spectrogramme résiduel, différence entre les données combinées et le modèle estimé.

L'inspection de ces résidus renseigne sur les éventuelles imprécisions des à priori , et ouvre la voie à leur correction (de manière similaire à ce qui a été présenté pour la caractérisation des raies photosphériques des étoiles standard, une gaussienne remplaçant la lorentzienne).

La procédure s'applique aux spectrogrammes de science comme aux spectrogrammes d'étoiles standard. Dans ce dernier cas, la quantité de signal et l'absence d'objets de champs la rend plus robuste. Les exemples illustratifs seront donc empruntés aux étoiles standard.

4.3.1 Intégration par régions

Afin d'accroître le signal résiduel par rapport au niveau de bruit, le spectrogramme résiduel est intégré selon X dans des régions telles que le signal obtenu soit $ N_{\sigma}$ =20 fois le niveau de bruit.

En fait, comme le signal résiduel peut être négatif ou positif, le niveau de signal est défini comme la somme des valeurs absolues des pixels déviant de plus d'une fois le bruit propagé local, et le niveau de bruit comme la somme quadratique du bruit propagé des pixels composant le niveau du signal. Ce critère est atteint pour un pur bruit gaussien en 1.355 $ \times N_{\sigma}^2$ , soit pour 540 pixels avec une coupure à 20, ou une dizaine de colonnes pour une fenêtre d'extraction large de 50 pixels (FWHM = 5 pixels = 1'').

Pour les spectrogrammes d'étoile standard, un rapport de 200 est utilisé, mais l'on pourrait aussi bien s'abstenir d'intégrer.

4.3.2 Correction de la position

Dans l'hypothèse d'une PSF gaussienne $ \mathcal{N}$ , d'intensité totale $ I$ et d'écart-type $ \sigma $ , une erreur $ \delta $ Y sur la position $ Y_s$ du point source se traduit sur le spectrogramme résiduel par un profil selon Y proportionnel à la dérivée selon Y de la PSF. Le coefficient de proportionnalité est opposé au décalage $ \delta $ Y dans une approximation linéaire valable pour de petits décalages ($ \delta $ Y $ \ll \sigma$ ):

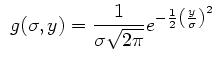   soit $\displaystyle y={\tt Y}-Y_s $   , et $\displaystyle \ g(\sigma, y)=\frac{1}{\sigma \sqrt{2\pi}}e^{-\frac{1}{2}\left(\frac{y}{\sigma}\right)^2 }$    la gaussienne normalisée ;

pour une PSF vraie : $\displaystyle \mathcal{N}=I g(\sigma, y)$    et une PSF modèle : $\displaystyle \mathcal{M}=I g(\sigma, y-\delta y)$    ,

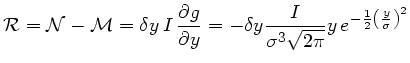
   le résidu vaut $\displaystyle \mathcal{R}=\mathcal{N}-\mathcal{M}=\delta y I \frac{\partia... ...ac{I}{\sigma^3 \sqrt{2\pi}} y e^{-\frac{1}{2}\left(\frac{y}{\sigma}\right)^2} $

Si l'on définit le calibre $ \mathcal{Q}_y$ adapté à la quantification des $ \delta y$ :

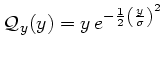
$\displaystyle \mathcal{Q}_y(y) = y e^{-\frac{1}{2}\left(\frac{y}{\sigma}\right)^2} $

et sa norme comme l'intégrale de son carré $ q_y = \int Q_y(y)^2 dy$ , l'intégrale du produit du calibre avec le résidu s'écrit :

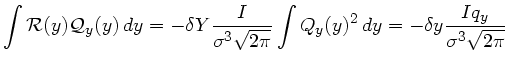
$\displaystyle \int \mathcal{R}(y)\mathcal{Q}_y(y) dy = -\delta Y \frac{I}{\sigma^3\sqrt{2\pi}} \int Q_y(y)^2 dy = -\delta y \frac{ I q_y}{\sigma^3\sqrt{2\pi}} $

Donc, à supposer une PSF gaussienne, dont on connait les paramètres $ Y_s$ et $ \sigma $ à priori, et $ I$ par extraction de PSF, on peut calculer le calibre $ \mathcal{Q}_y$ , sa tare $ q_y$ , et l'intégrale de son produit avec le profil résiduel. En multipliant cette dernière par $ n_y = \sigma^3\sqrt{2\pi}/( I q_y )$ , on obtient la correction -$ \delta $ Y a appliquer à l'à priori $ Y_s$ .

Lorsque $ \delta $ Y n'est pas négligeable devant $ \sigma $ , le résidu n'est plus proportionnel à la dérivée (au calibre), et l'estimateur devient non-linéaire.

Vérification sur l'étoile standard HD49798 :

Pour tester cet estimateur, voyons l'effet d'une mésestimation volontaire de 1 pixel, pour le spectrogramme de l'étoile standard HD49798, acquise 7h30 après 04D4it (c.f. Fig. 4.10). Les à prioris de départ $ Y_s$ , $ \alpha $ , $ \sigma _0$ et $ \kappa$ sont calculés d'après les moments des profils intégrés dans 10 régions selon X. Un décalage $ \delta $ Y de 1 pixel ( $ \sim \sigma_0$ /2) est introduit avant l'extraction de PSF d'une seule composante gaussienne (cas des étoiles standard). On fait l'hypothèse que l'échantillonnage est suffisant, pour utiliser la valeur du calibre au centre du pixel plutôt que son intégrale sur la hauteur du pixel.

Figure 4.10: Image : Grille des résidus obtenus en rééchantillonnant selon X en 228 régions, dans la fenêtre d'extraction à $ \pm $ 5 FWHM (52 pixels selon Y). À gauche : Coupe selon Y, en $ X_0$ , et le calibre utilisé, centré sur la position à priori $ Y_s$ (en pointillés), et de $ \sigma $ égal à celui estimé sur le profil intégré. Le calibre est arbitrairement amplifié. Au centre : Ajustement linéaire des produits normalisés $ n_y \int \mathcal{R}\times\mathcal{Q}_y$ en fonction de X. Les barres d'erreur sont inversement proportionnelles à la racine du rapport [flux extrait / bruit propagé] dans la région (du poids assigné aux régions lors de l'ajustement). Leur normalisation est arbitraire. À droite : Effet de l'imprécision $ \delta $ Y sur le spectre extrait par PSF gaussienne. Le rapport moyen entre le spectre extrait original et celui affecté est de 0.94 .
Illustration de la correction de $ Y_s$ , avec $ \delta $ Y=1 pixel.
Image Std_dy1_resgrid
Image Std_dy1_rescut Image Std_dy1_fitpos Image Std_dy_on_spec

On constate que l'algorithme fonctionne bien, même pour un décalage de $ \sim \sigma$ /2, 20 % du seeing $ w_0$ . La correction estimée comme la valeur de l'ajustement selon X en $ X_0$ est de -0.96 pixel, à 4 % de l'imprécision introduite (c.f. Fig. 4.10-b). L'effet du décalage sur le spectre extrait est une sous-estimation de 6 % en moyenne, faible comparée à l'amplitude de l'erreur.

Il apparaît également que la coupe du résidu n'est pas homothétique par rapport au calibre. Cela dénote que l'approximation gaussienne n'est pas exacte.

Correction de l'inclinaison :

L'ajustement réalisé sur la correction estimée en chaque X fournit la correction à appliquer à $ Y_s$ , mais aussi à l'inclinaison $ \alpha $ .

En fait, il est plus sain de corriger d'abord l'estimée de $ Y_s$ , puis de recommencer l'exercice pour corriger $ \alpha $ séparément. On évite ainsi les possibles dérives dûes à la mésestimation de $ Y_s$ et à la non-linéarité de l'estimateur.

4.3.3 Correction du seeing

On procède de manière similaire pour estimer l'imprécision $ \delta \sigma$ sur $ \sigma _0$ , et $ \delta \kappa$ sur $ \kappa$ . Pour un modèle $ \mathcal{M}$ affecté d'une imprécision $ \delta \sigma$ , on écrit cette fois :

$\displaystyle \mathcal{M}=I g(\sigma+\delta \sigma, y) $

$\displaystyle \mathcal{R}=\mathcal{N}-\mathcal{M}=-\delta \sigma I \frac{\... ... \frac{g(\sigma,y)}{\sigma} \left[ \left(\frac{y}{\sigma}\right)^2-1 \right] $

Le calibre $ \mathcal{Q}_{\sigma}$ adapté devient $ \mathcal{Q}_{\sigma}(y) = [ (y/\sigma)^2-1 ] e^{-1/2 (y/\sigma)^2} $ , dont la norme vaut $ q_{\sigma}$ . Celle du résidu avec le calibre vaut alors

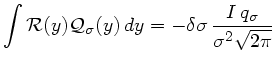
$\displaystyle \int \mathcal{R}(y)\mathcal{Q}_{\sigma}(y) dy = -\delta \sigma \frac{I q_{\sigma}}{\sigma^2\sqrt{2\pi}} $

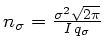Une fois encore, le calcul de cette intégrale, normalisé par $ n_{\sigma} = \frac{\sigma^2\sqrt{2\pi}}{I q_{\sigma}}$ fournit la correction à apporter à $ \sigma _0$ , en chaque région. L'ajustement de ces corrections en fonction de $ \lambda $ permet d'estimer la correction $ \delta \sigma_0$ en $ X_0={\tt X}(\lambda_0)$ . Un développement linéaire de $ \sigma (\lambda )$ fournit la correction à effectuer sur $ \kappa$ en fontion de la pente $ b$ de l'ajustement :

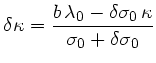
$\displaystyle \delta\kappa= \frac{b \lambda_0-\delta\sigma_0 \kappa}{\sigma_0+\delta\sigma_0}$

Les résultats obtenus pour une surestimation volontaire du seeing $ w_0$ de $ \delta \sigma$ =0.5 pixel ($ \sim $ 10 % de $ \sigma _0$ ) sont présentés en figure 4.11 (Pour un profil gaussien, on a la relation suivante entre le seeing (FWHM) et l'écart-type : $ w = 2 \sqrt{2 \ln(2)} \sigma$ = 2.355 $ \sigma $ ).

Figure 4.11: (Idem Fig. 4.10) Image : Grille des résidus obtenus en rééchantillonnant selon X en 47 régions. Au centre : Coupe selon Y, en $ X_0$ , et le calibre $ \mathcal{Q}_{\sigma}$ utilisé. À droite : Ajustement linéaire des corrections 2.355 $ n_{\sigma} \int \mathcal{R}\times\mathcal{Q}_{\sigma} dy$ en fonction de $ \lambda $ .
Illustration de la correction de $ w_0$ , avec $ \delta w$ =0.5 pixel.

Image Std_dw1_resgrid Image Std_dw1_rescut Image Std_dw1_fitwid

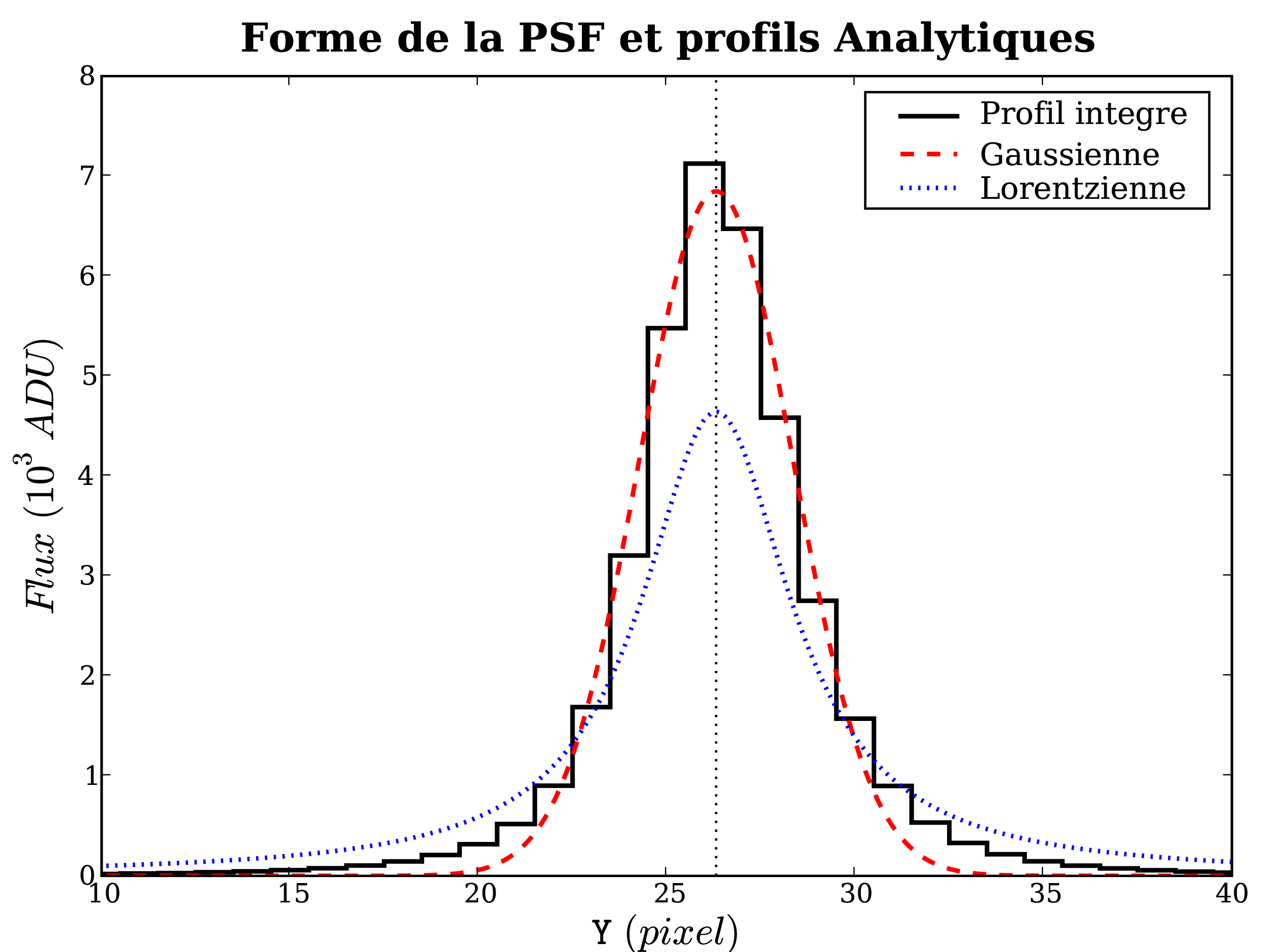
On constate que la correction n'atteint que 60 % de l'imprécision. Ceci est dû à l'hypothèse de PSF gausienne, alors que la vraie PSF a des ailes plus larges (qui apparaissent sur le résidu au-delà de FWHM $ \sim $ 5 pixels du centre : il redevient positif).

Le spectre extrait en surestimant ainsi $ \sigma _0$ est aussi surestimé, de 5 %. L'extraction de PSF est donc plus sensible à une mauvaise estimation de $ \sigma _0$ que de $ Y_s$ , et le calibre $ \mathcal{Q}_{\sigma}$ moins efficace que $ \mathcal{Q}_y$ .

4.3.4 Correction itérative

Ces corrections sont répétées successivement ($ Y_s$ , $ \alpha $ puis $ \sigma _0$ et $ \kappa$ ), jusqu'à ce qu'elles soient petites ($ \sim $ 10%) par rapport à leur imprécision propre, estimée lors des ajustements, ou qu'elles oscillent. L'extraction est refaite à chaque actualisation des à priori.

Pour l'étoile standard présentée, la convergence est obtenue en une itération pour la position et la largeur, et en trois pour l'inclinaison. Les correction apportées sont minimes car les à prioris, obtenus d'après les profils intégrés dans 10 régions, sont déjà bons. La correction a pour effet de se focaliser sur le c\oeur du profil. La table 4.12 résume les corrections obtenues :

Figure 4.12: Image de gauche: Résidus originaux, rééchantillonnés en 41 régions, dévoilant l'écart de la vraie PSF au meilleur modèle gaussien. Table : Corrections calculées pour l'extraction du spectre de HD49798. Image de droite: Résidus finaux, rééchantillonnés en 42 régions, très proches des originaux.
Image Std_simple_resgrid
Variable $ Y_s$ (pixel) $ \alpha $ (10$ ^{-3}$ ) $ w_0$ (pixel) $ \kappa$
Iterations 1 3 1 1
Originale 100.34 0.348 4.771 -0.348
Correction +0.01 -0.006 -0.038 -0.013
Finale 100.35 0.342 4.733 -0.361
Image Std_iter_resgrid

L'effet des corrections sur le spectre extrait est négligeable (-0.4 %, imputable à la réduction de $ \sigma _0$ ), de même que sur l'écart-type des résidus (-0.7 %). On les effectue tout de même lors de l'extraction des spectres d'étoiles standard, pour minimiser les résidus dans le cadre de l'hypothèse d'une PSF gaussienne. En effet, comme l'à priori est initalement construit d'après les profils intégré dans $ \sim $ 200 pixels, l'étalement risque être surestimé à cause de l'inclinaison de la trace.

L'amplitude maximale des résidus dans une colonne est d'environ 1.4 % du flux total ($ \sim $ 930/67000), le flux résiduel moyen est de $ \sim $ +0.3 % (220/67000), et l'écart-type est de 0.7 % (470/67000), provenant principalement de la non-gaussiannité de la PSF (c.f. Fig. 4.13). La courbure de la trace est ici secondaire, sauf aux $ \lambda $ extrêmes, où le flux est faible (c.f. Fig. 4.10-b). Pour réduire d'avantage les résidus, il faut raffiner le modèle de la trace (coefficients polynomiaux d'ordre superieur) et celui de la PSF (base de fonction ayant plus de paramètres, i.e. les fonctions Moffat qui peuvent être piquées et étendues, avec 3 paramètres).

Image Std_ProfilComp
Figure 4.13: Comparaison du profil intégré dans la région de $ X_0$ avec le modèle gaussien estimé, et le profil lorentzien de même intégrale et largeur à mi-hauteur.
 

Application aux supernovæ :

Dans le cas des spectrogrammes de supernova, le niveau du signal est bien moindre, et la source n'est généralement pas seule. On peut donc craindre un comportement chaotique de la correction itérative, induit par le bruit, ou déviant, à cause d'un hôte chromatique proche, mal soustrait, qui polluerait l'estimation de la correction.

Cependant, les à prioris obtenus par le seeing synthétique dérivé des observations de l'étoile guide et par l'adéquation spectro-photométrique sont vraisemblablement moins précis que ceux obtenus directement du spectrogramme pour les étoiles standard. L'indice $ \kappa$ est imposé à -0.2, alors qu'il vaut plutôt -0.3 d'après les observation d'étoiles standard. En fait, celles-ci étant prises avec des temps d'exposition courts (de 0.7 sec. à 3 min.), les propriétés de leur PSF risquent d'être différentes de celles d'une observation de 15 min., à cause de la turbulence et/ou du guidage. Il arrive de voir des PSF asymétriques, voir dédoublées.

La correction iterative n'est pas appliquée systématiquement aux spectrogrammes de supernovæ. Elle est néanmoins applicable au cas par cas si le spectrogramme résiduel montre une imprécision flagrante. En général, la réduction des résidus est imperceptible, noyée dans le bruit.

Dans le cas de 04D4it, la faiblesse du signal et la présence d'une galaxie proche sont de mauvaise augure. Toutefois, la correction iterative converge relativement sainement.

Figure 4.14: Image de gauche: Résidus originaux, rééchantillonnés en 125 régions de 42 lignes. Image de droite: Résidus finaux, rééchantillonnés en 126 régions. Table : Corrections calculées pour l'extraction de la supernova 04D4it.
Image 04D4it_direct_resgrid
$ \quad \Rightarrow \quad$
Image 04D4it_iter_resgrid
Variable $ Y_s$ (pixel) $ \alpha $ (10$ ^{-3}$ ) $ w_0$ (pixel) $ \kappa$
Iterations 2 3 2 2
Originale 96.83 -1.588 4.131 -0.200
Correction -0.32 +0.769 -0.015 +0.402
Finale 96.51 -0.819 4.116 +0.202

Le spectre extrait après correction est légérement plus faible (-7 %), et présente une variance plus grande. L'écart-type des résidus sur toute la fenêtre d'extraction passe vaillement de 3.995 ADU à 3.990, une baisse de 0.1 %. L'obtention d'un indice $ \kappa$ positif est révélatrice de la fiabilité douteuse de la correction à bas signaux.

next up previous contents
Next: 4.4 Les touches finales Up: 4. Jouer toutes ses Previous: 4.2 Limites de la
Sylvain Baumont
2010-01-11