La technique présentée a l'avantage d'une relative simplicité (et rapidité d'execution), et le potentiel de séparer efficacement le spectre de la supernova de celui de sa galaxie hôte. Cependant, les hypothèses faites ne sont pas toujours exactes.
Les raies d'émission nébulaire proviennent de régions périphériques de formation
d'étoiles, et dominent le profil à leur ![]() d'émission (c.f. Figure 4.5).
Le profil y est alors encore plus excenté, et une troisième composante
serait nécessaire pour pouvoir le reproduire.
d'émission (c.f. Figure 4.5).
Le profil y est alors encore plus excenté, et une troisième composante
serait nécessaire pour pouvoir le reproduire.
|
Plus subtilement, la vitesse de rotation de galaxies observées par la tranche
modifie, par effet Doppler, le ![]() de la lumière émise.
Ainsi, les raies d'émission et d'absorption apparaîtront inclinées sur
le spectrogramme (le côté approchant est bleui, celui qui s'éloigne est rougi).
de la lumière émise.
Ainsi, les raies d'émission et d'absorption apparaîtront inclinées sur
le spectrogramme (le côté approchant est bleui, celui qui s'éloigne est rougi).
Ce chromatisme n'est bien sûr décelable que pour les galaxies résolues. L'inexactitude du modèle se reflète sur le spectrogramme résiduel de l'extraction, qui peut être analysé postérieurement pour mesurer plus précisément l'intensité des raies nébulaires et la vitesse de rotation radiale.
Il n'est pas rare qu'une galaxie de champ apparaisse, par projection, en contact avec
la galaxie hôte observée (c.f. Fig. 4.6 ).
En ce cas, l'algorithme les traite comme un unique objet.
Si les galaxies sont à des distances, à des redshifts, différents, leurs couleurs seront
différentes et l'objet sera de type mixte. La galaxie la plus lumineuse jouera le rôle
de c![]() ur ponctuel, et tout ce qu'il reste alentour jouera le rôle des bras spiraux.
En particulier, le résidu du côté opposé à la galaxie voisine fera partie de la
même composante qu'elle.
ur ponctuel, et tout ce qu'il reste alentour jouera le rôle des bras spiraux.
En particulier, le résidu du côté opposé à la galaxie voisine fera partie de la
même composante qu'elle.
|
|
Ce problème peut être résolu manuellement en éditant le fichier fournissant les profils des composantes au programme d'extraction, pour y mettre à zéro la partie indésirable.
Ainsi, les coordonnées enregistrées dans la base de données commune franco-canadienne ne sont pas alignées avec les dernières versions des images profondes. Un écart de quelques pixels apparaissait fréquemment.
En fait, la minimisation du ![]() s'accommode d'un écart inférieur à
s'accommode d'un écart inférieur à
![]() , mais un biais apparaît à cause de la variation de
, mais un biais apparaît à cause de la variation de ![]() avec
avec ![]() .
D'autre part, le calcul de l'inclinaison
.
D'autre part, le calcul de l'inclinaison ![]() devient hasardeux, puisque le maximum
de corrélation sera déterminé par le plus intense de la supernova ou de la galaxie,
sujet à changer d'un filtre à un autre.
devient hasardeux, puisque le maximum
de corrélation sera déterminé par le plus intense de la supernova ou de la galaxie,
sujet à changer d'un filtre à un autre.
L'utilisation des coordonnées recalculées pour la construction des courbes de lumières, cohérantes avec l'astrométrie des images profondes, a réduit ce problème.
|
|
En conséquence, si la galaxie hôte est trop petite et lointaine pour être résolue, et que la supernova n'est pas suffisement excentrée, le couple supernova+galaxie sera brouillé en un unique point source. Toute tentative de séparation des deux composantes sera alors vouée à l'échec.
C'est le cas de 04D4it, malgré une qualité d'image effective respectable de 0.81'' (c.f. Fig. 4.8). Plus le redshift est élevé, plus ce problème est répandu. Sauf pour les supernovæ dont l'hôte est trop faible pour être décelé (supernovæ orphelines).
La fusion de ces supernova avec leur galaxie ne résoud pas le problème, puisque l'on renonce à séparer quoi que ce soit.
|
|
La position de la trace est liée à une combinaison de la dispersion atmosphérique4.3résiduelle (non corrigée par l'Atmospheric Dispersion Compensator qui équipe les télescopes modernes), et de la torsion entre le grisme et le CCD. Pour FORS1, cette torsion est vraisemblablement négligeable.
La largeur de la trace, elle, est une combinaison de
![]() et des
aberrations optiques de l'instrument.
et des
aberrations optiques de l'instrument.
Lors de l'extraction du spectre des étoiles standard par la méthode des moments,
la position et la largeur de la PSF sont estimées en chaque ![]() .
Cet échantillon d'observations de sources brillantes permet de quantifier
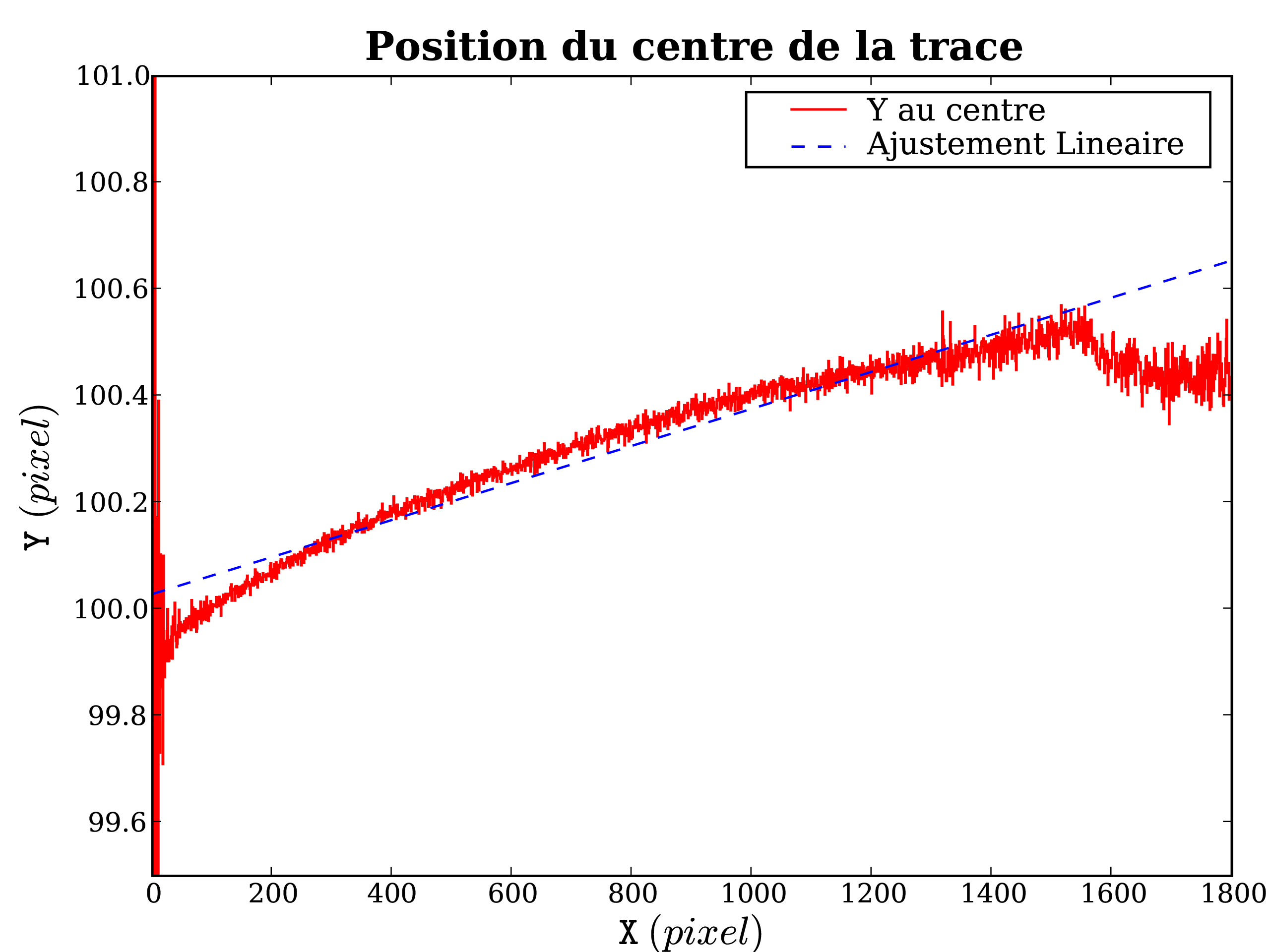
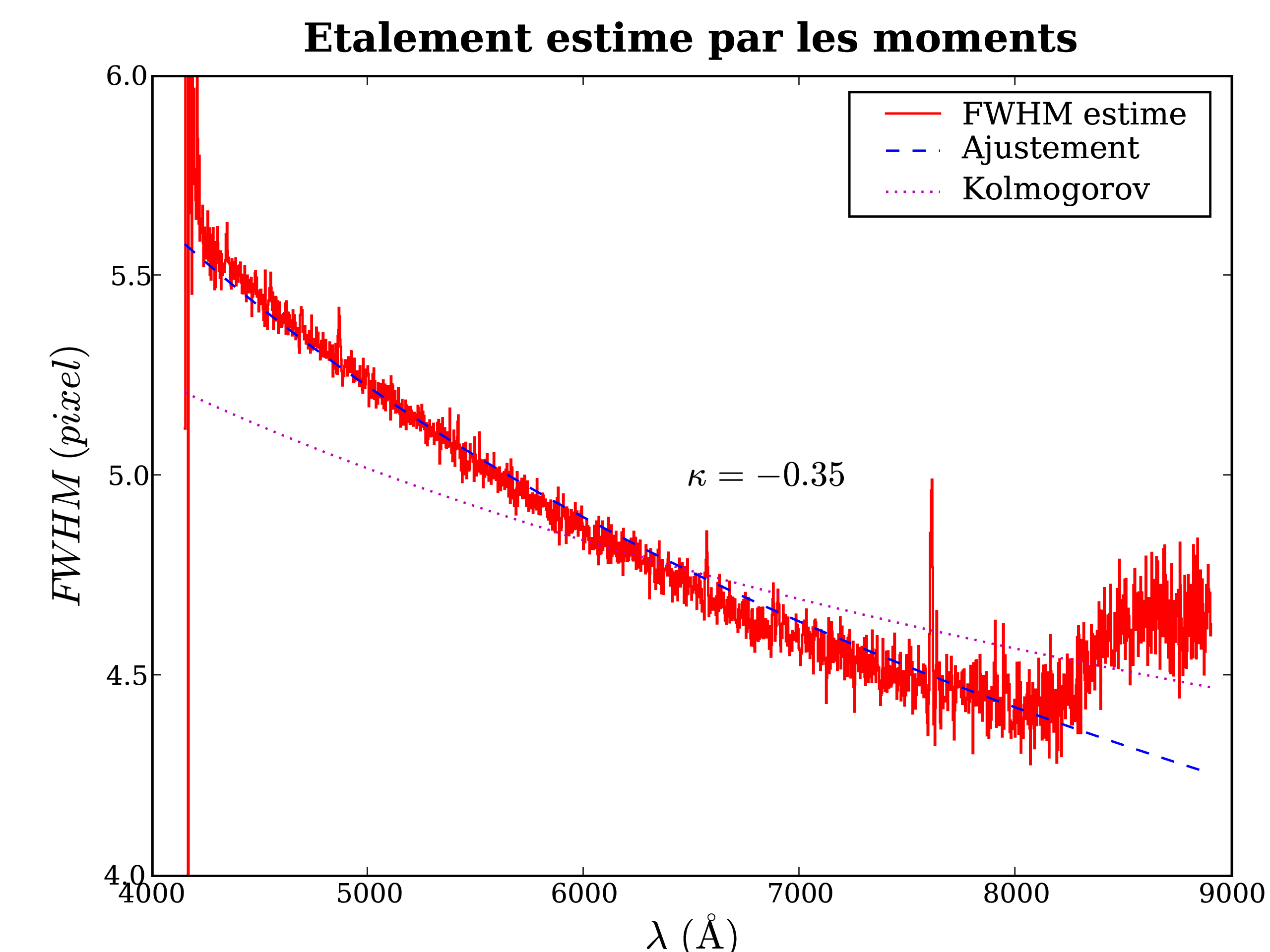
l'imprécision de notre modèle (c.f. Fig. 4.9).
.
Cet échantillon d'observations de sources brillantes permet de quantifier
l'imprécision de notre modèle (c.f. Fig. 4.9).
|
On constate qu'effectivement, la théorie de Kolmogorov n'est pas vraiment adéquate,
et que l'indice de la loi de puissance est plutôt de -0.3 .
La position de la trace n'est pas exactement linéaire, et serait mieux reproduite
par une parabole.
Cependant, l'écart à la linéarité est faible (![]() 0.1 pixel), et dans le cas
de faibles flux il est improbable de bien estimer une parabole avec nos 3 décalages.
0.1 pixel), et dans le cas
de faibles flux il est improbable de bien estimer une parabole avec nos 3 décalages.
La contamination par le second ordre de diffraction est évidente au-delà de 8200 Åpour cet objet très bleu, mais sera complétement négligeable pour les supernovæ lointaines, faibles et rougies.