Next: 4.2 Limites de la Up: 4. Jouer toutes ses Previous: 4. Jouer toutes ses

4.1 Les grandes lignes

La motivation principale pour raffiner l'extraction est d'obtenir, directement depuis le spectrogramme bidimensionel, un spectre de supernova pur. L'ajustement de modèles de galaxies en sus de ceux de supernovæ pour classifier l'objet source sera alors inutile, et l'imprécision propre à la soustraction de ces modèles discrets sera abolie.

Cependant, il est illusoire d'atteindre cette pureté pour tous nos candidats. Mais, lorsque cela est possible, il faut pouvoir le faire.

4.1.1 Obtention des à priori

Le plan d'attaque du problème est le suivant : On veut comparer les profils d'intensité intégrés dans les filtres du CFHT avec ceux auxquels on s'attend si le pointage du VLT est précisement celui demandé : aux coordonnées de la supernova.

De cette comparaison, on pourra dériver la position exacte de la supernova sur le spectrogramme, et utiliser cette information pour n'extraire le signal qu'en cette position.

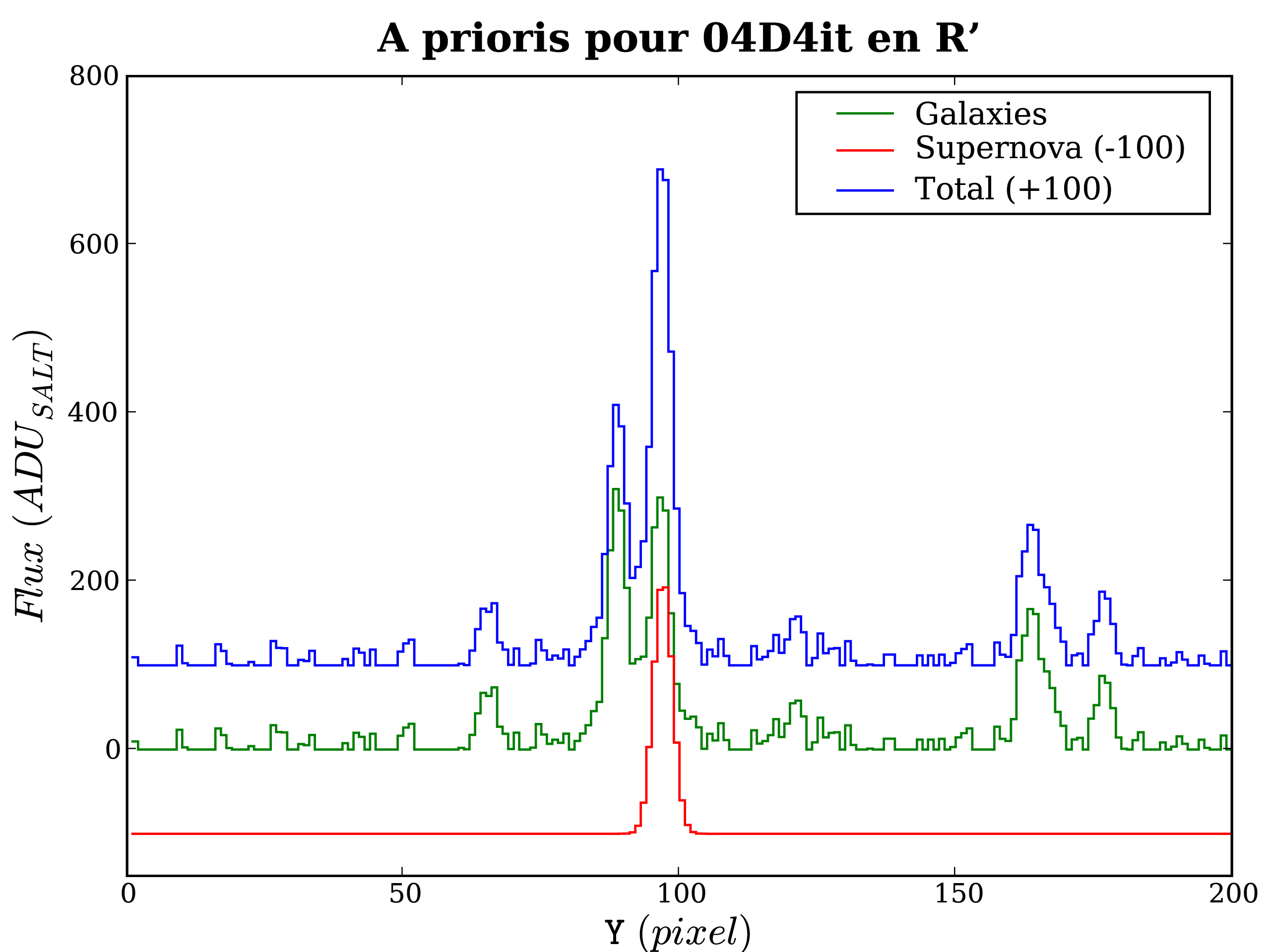
Le profil photométrique comporte d'une part les sources stables, les galaxies, et d'autre part le transient ponctuel identifié. Pour pouvoir réaliser des courbes de lumière de précision cosmologique et trouver efficacement les nouveaux transients, le groupe de photométrie construit les images profondes des 4 champs de 1 degré carré observés (de 20k x 20k = 400 Mega-pixels). Idéalement, le flux des objets variables doit être exclu de ces images, mais la mise en $\oe$ uvre d'un tel filtre est complexe, et l'on utilise plutôt les références passées ou futures pour (re)trouver les objets. Les courbes de lumière précises sont obtenues en réalignant toutes les images disponibles pour construire la référence locale contemporaine et la courbe de lumière du point source recherché, entre -30 et +150 jours autour du maximum de luminosité, dans chaque filtre.

Par une coupe photométrique :

Nous disposons donc de deux sources possibles du profil galactique : les grands champs profonds, ou les vignettes réalignées propres à chaque supernova.

Dans les deux cas, il faut intégrer ces images le long de la fente projetée sur la voute céleste. En supposant un pointage parfait, et connaissant l'angle polaire d'observation, cette fenêtre d'intégration est facile à définir (c.f. Fig. 4.1). Plus complexe est l'intégration selon une grille inclinée par rapport à celle des pixels. J'ai utilisé le programme spécialisé SWarp (E. Bertin) du groupe de traitement des images de MegaCam TERAPIX^4.1pour effectuer ce rééchantillonnage. Le pixel de référence $Y_{ref}$ est associé aux coordonnées de la supernova.

Toujours soucieux du niveau de bruit des modèles, les coupes obtenues sur les images profondes sont préférées à celles des vignettes. Pour que la supernova n'apparaisse pas diluée sur la coupe, j'utilise les champs profonds les moins contemporains de la supernova.

Et le flux de la supernova :

Le flux des candidats dans chaque filtre est mesuré tous les 4 jours, lorsque la météo le permet. Le flux $\hat{F}_{spec}$ au moment de l'observation spectroscopique peut être grossièrement approximé par interpolation linéaire des mesures photométriques prises avant et après.

Par ailleurs, J. Guy a développé un modèle de courbes de lumières de SN-Ia : SALT (pour Spectral Adaptive Light-curve Template [5]), qui permet d'ajuster simultanément les courbes de lumières dans tous les filtres, connaissant le redshift, et à supposer que le candidat est effectivement une SN-Ia. En fait, la qualité de l'ajustement est révélatrice de la probabilité qu'il en soit une.

Pour les candidats déjà estampillés SN-Ia par l'analyse en temps-réel, cet ajustement fournit une estimation plus fine de la luminosité du transient au moment de la spectroscopie.

Lorsque cet ajustement n'est pas disponible, l'interpolation des points de photométrie est utilisée. Cependant, s'il n'y a de mesures qu'avant la date de spectroscopie, et que le transient déclinait déjà, l'extrapolation peut mener à un flux négatif. Dans un tel cas, un flux arbitrairement faible (20 $ADU_{SALT}$ et un point zéro de 30, soit une magnitude $\sim$ 26.75) est utilisé.

.

Pour additionner ces deux composantes, il faut auparavant les exprimer dans la même unité. Les points zéro associés aux deux mesures (aux deux unitées $ADU_{CFHT}$ et $ADU_{SALT}$ ) permettent de convertir une unité en l'autre. On choisit le point zéro (

) le plus grand : celui des courbes de lumière, et le profil photométrique est multiplié par $10^{\frac{ ZP_{SALT}-ZP_{CFHT} }{2.5} }$ .

Le point source du candidat y est ajouté sous la forme d'une gaussienne d'intégrale $\hat{F}_{spec}$ , de largeur égale au seeing ( $\sigma = \frac{seeing}{2\sqrt{2\log2}}$ ), et centrée sur la position du candidat (c.f. Fig 4.3-a).

**Figure 4.3:** **À gauche :** Exemple d'à priori obtenu pour le candidat 04D4it, dans le filtre r'. **À droite :** Calage des profils à priori (CFHT) sur les profils intégrés (VLT), pour les trois filtres. Les décalages $\Delta Y$ trouvés pour chaque filtre sont indiqués. On en déduit =97.83 pixel (dans le referenciel du spectrogramme combiné), et $\alpha$ =-1.59 10 $^{-3}$ .

4.1.2 Adéquation spectro-photométrique

Si la précision absolue de pointage du VLT était inférieure à 0.2'' (au pixel), on pourrait utiliser directement cet à priori pour guider l'extraction. Comme ce n'est pas le cas, il est nécessaire de caler le profil à priori sur le profil intégré (c.f. Fig. 4.3-b).

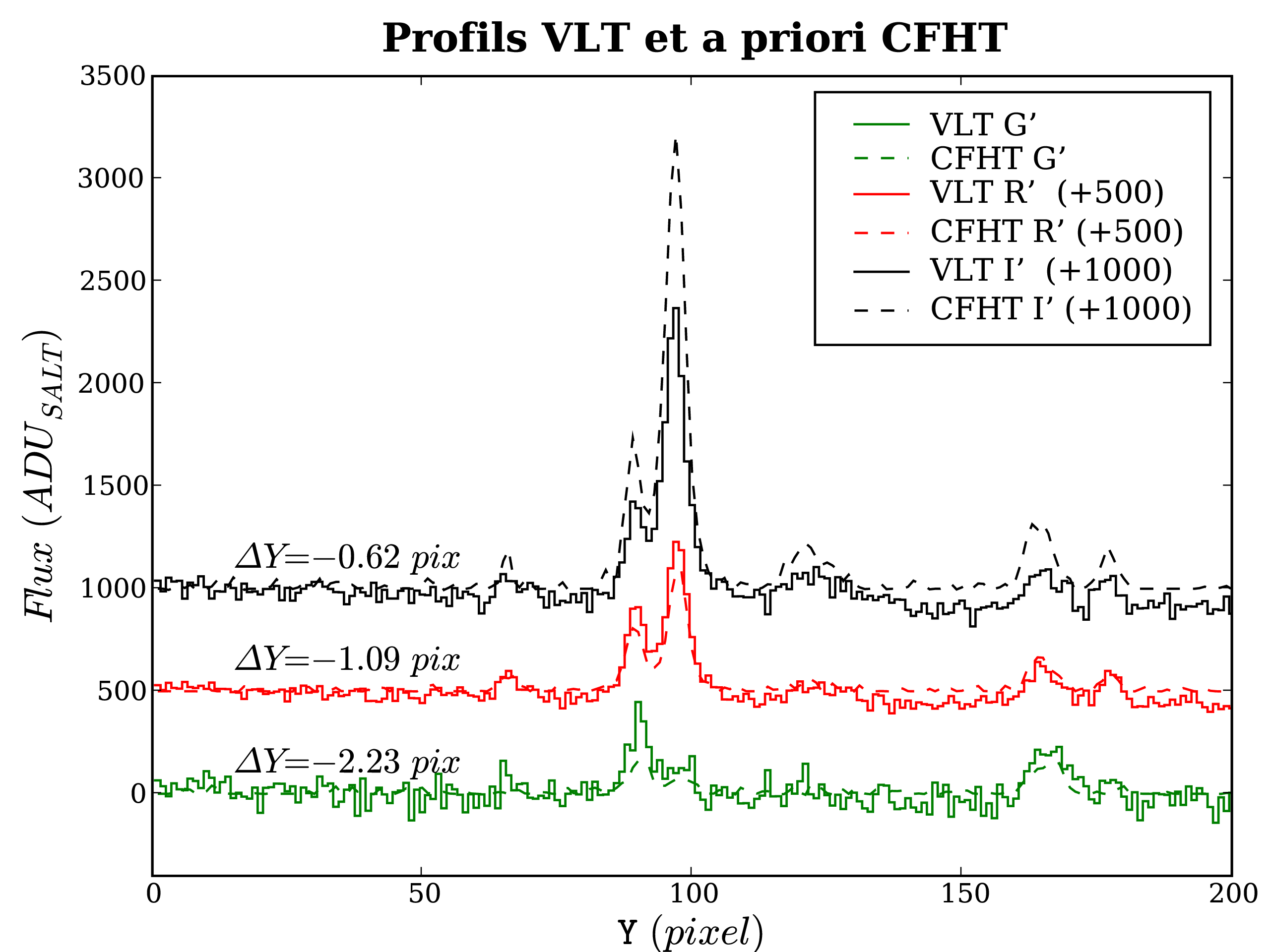
Pour ce faire, la corrélation des deux profils est calculée, et la position de son maximum parabolique est estimée (théoriquement égale au décalage entre les deux profils), pour chaque filtre.

On obtient donc 3 décalages $\Delta Y_k$ entre les profils intégrés et l'à priori, valables aux 3 $\lambda_k$ effectifs des 3 filtres (pour le grisme 300V; 2 pour le 300I). Un ajustement linéaire de ces décalages en fonction de X fournit l'estimée de la position du candidat en et de l'inclinaison $\alpha$ de sa trace :

$\displaystyle \Delta Y_k = (Y_s-Y_{ref}) + \alpha \times ({\tt X}(\lambda_k)-X_0)$

Lors de l'ajustement, les décalages sont pondérés par la valeur de la réponse instrumentale, intégrée dans chaque filtre. On donne ainsi plus de poids aux décalages calculés là où la fonction de réponse est la plus grande, donc là où l'on s'attend à avoir le plus de flux.

Les profils intégrés sont normalisés aux mêmes flux totaux que les profils à priori, dans l'unique but de rendre agréable la visualisation du calage.

Robustification aux faibles flux :

En fait, lorsque le candidat est très faible, le niveau de bruit des profils est supérieur au signal, et la corrélation est dominée par ce bruit. Son maximum risque alors de se trouver là où les bruits, plutôt que les signaux, se corrèlent le mieux, aboutissant à un décalage erronné.

Afin de limiter la contribution du bruit, les valeurs négatives des profils sont mises à zéro avant d'effectuer la corrélation (visible en Fig. 4.3-a).

Lorsque la pente $\alpha$ est trop forte ( 6 pixels bord à bord), car il n'y a précisément pas de assez de signal dans une ou plusieurs bandes, cette pente est forcée à zéro et la position estimée au centre est utilisée. Notons que s'il n'y a pas assez de flux pour retrouver la position de la source, cela est de mauvais augure pour l'extraction à venir.

4.1.3 Définition des sources à extraire

À présent que l'on a fait le lien entre les références photométriques et notre spectrogramme, il nous faut définir la position et le profil spatial des sources à extraire. Cette étape est d'une importance cruciale car elle conditionne la qualité des spectres qui seront extraits.

En effet, il nous faut décomposer le profil galactique en composantes élémentaires : en sources dont le spectre est uniforme. Cependant, l'information spectrale est contenue dans le spectrogramme combiné, duquel on veut l'extraire. L'exercice consiste donc à définir le plus précisément possible ces composantes à partir des seuls profils photométriques, pris dans différents filtres, c'est à dire intégrés dans divers domaines spectraux.

Le cas de figure le plus général correspond à une supernova explosant au sein des bras d'une galaxie spirale. Étant donné que les bras spiraux sont constitués d'une population d'étoiles plus jeunes que celle du c $\oe$ ur, contenant plus d'étoiles massives et chaudes, le spectre des bras est plus bleu que celui du c $\oe$ ur, et contient également des raies d'émission nébulaire (raies de désexcitation de nuages de gaz éclairés par le rayonnement dur d'étoiles chaudes proches), indicateur d'une phase de formation stellaire récente. On dénombre alors au moins trois composantes élémentaires : le c $\oe$ ur de la galaxie, ses bras spiraux et la supernova.

Il est également fréquent que d'autres galaxies, situées ou non à la même distance que la supernova, se trouvent dans la fente. Il faut en ce cas séparer chaque galaxie en une composante (ou deux si c'est une galaxie spirale).

L'algorithme d'extraction présenté ci-après se base sur le profil des sources à extraire pour calculer leur flux en chaque colonne du spectrogramme combiné (en chaque $\lambda$ ), par minimisation du $\chi ^2$ .

La supernova est une source ponctuelle, non résolue. Son profil est supposé être gaussien (PSF), de largeur à mi-hauteur égale au seeing mesuré par la caméra de guidage de l'UT au cours de l'observation spectroscopique (à Paranal).

Concernant les galaxies, on distinguera trois types de sources :

$\bullet$

Les sources non résolues ( ponctuelles ) :

Ce sont les galaxies trop petites et/ou trop lointaines, dont l'étendue sur les images de référence est du même ordre de grandeur que le seeing. Le profil considéré est également gaussien, mais de largeur à mi-hauteur égale au seeing des images de référence.

$\bullet$

Les sources étendues uniformes :

Ce sont les galaxies résolues, ne présentant pas de différence de couleur entre leur c $\oe$ ur et leurs bras. Cela correspond usuellement à des galaxies ellipiques, n'ayant pas connu de phase de formation stellaire depuis longtemps, par manque de réservoir de gaz. Le profil supposé correspond alors au profil moyen déduit des images de référence, dans les filtres couverts par le spectrogramme.

$\bullet$

Les sources mixtes :

Ce type de source est destiné à représenter les galaxies spirales. Contrairement aux deux types précédents, qui associent une unique composante à un objet astrophysique donné, celui-ci décompose la galaxie en deux composantes : Un c $\oe$ ur non résolu, et son complément étendu. La somme des profils des deux composantes étant égal au profil moyen dans les filtres couverts. D'un point de vue algorithmique, lors de l'extraction, ce type de source est simplement considéré comme deux sources distinctes, l'une étant ponctuelle, et l'autre étant étendue.

Mise en oeuvre :

L'implémentation de cette décomposition du profil galactique, pourtant unidimensionnel, en sources pertinentes n'a rien de trivial. Au terme de multiples essais, j'ai abouti à la procédure suivante, ayant 7 paramètres ajustables :

$\bullet$

Détection des sources :

Dans un premier temps, un filtre d'ondelette gaussienne adaptée au seeing des images de référence est appliqué au profil galactique bolométrique (moyenné sur tous les filtres couverts par le spectrogramme). La position des sources ayant un flux crête supérieur à $N_{\sigma}$ =8 fois l'erreur statistique sous-jacente est enregistrée. Si le flux crête déduit du profil filtré est supérieur à fois le flux crête du profil non filtré $F_{max}$ , la source est considérée comme ponctuelle, et étendue sinon (pour une source parfaitement gaussienne, le rapport est de 1, par construction de l'ondelette gausienne). La largeur à mi-hauteur des sources est calculée sur le profil initial, ainsi que l'extension à droite et à gauche des sources étendues, au delà desquelles le flux devient inférieur à = 0.05 fois $F_{max}$ .

$\bullet$

Groupement des sources :

Rien n'empêche de détecter plusieurs sources au sein d'un même objet astrophysique (typiquement : le c $\oe$ ur et les bras spiraux de part et d'autre). Pour optimiser l'extraction, il faut définir le nombre nécessaire et suffisant de composantes. Ainsi, l'on veut regrouper les sources spatialement distinctes si elles ont un spectre identique (tels les bras spiraux de chaque côté du c $\oe$ ur). À l'inverse, il faudra dissocier les sources proches ayant des spectres différents. Pour minimiser le nombre de sources, on fait l'hypothèse que les sources étant en contact font partie d'un même objet. La condition de contact est vérifiée si le centre d'une source est inclus dans l'extension d'une autre (l'extension d'une source ponctuelle est sa largeur à mi-hauteur). On regroupe ainsi toutes les sources trouvées en quelques objets, composés d'une ou de plusieurs sources, de types ponctuelle ou étendue.

$\bullet$

Caractérisation des objets :

Les objets ont été obtenus à partir du profil galactique bolométrique uniquement, car il continent tout le signal. Afin de savoir s'ils doivent être dissociés en plusieurs composantes, on se doit d'utiliser l'information de couleur contenue dans les profils galactiques pris dans différents filtres. Par souci de simplicité, on fait l'hypothèse que nos objets sont constitués d'un c $\oe$ ur entouré de bras spiraux, dont on veut comparer les couleurs : si elles sont différentes, leurs spectres le seront aussi. Si elles sont identiques, leurs spectres le seront probablement aussi. Ainsi, pour chaque objet, on identifie sa source la plus intense comme étant son c $\oe$ ur, ainsi que l'extension totale de toutes les sources le composant. Une gaussienne adaptée au seeing, centrée sur la position du c $\oe$ ur et d'amplitude crête égale à celle du c $\oe$ ur est soustraite du profil bolométrique ( en 300V), ainsi que des profils pris dans chaque filtre ( $f \in [g', r', i']$ ). Le flux alors contenu à l'intérieur de l'extension maximale est calculé, pour les profils résiduels bolométrique et de chaque filtre. On peut ainsi en déduire le rapport de flux entre le c $\oe$ ur et les bras, en moyenne (bolométrique), et dans chaque filtre. Une coupure est imposée en premier lieu sur le flux $B_{bolo}$ contenu dans les bras, relativement au niveau de bruit $\sigma_{B}$ et a celui du flux du c $\oe$ ur $C_{bolo}$ :

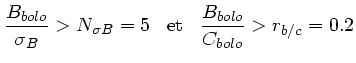
$\displaystyle \frac{B_{bolo}}{\sigma_{B}} > N_{\sigma B} = 5 \;\;\;{\rm et}\;\;\; \frac{B_{bolo}}{C_{bolo}} > r_{b/c}=0.2$

pour que l'objet ait une composante étendue ; puis sur la variance 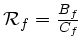$\sigma_c^2$ du rapport des flux ${\cal R}_f=\frac{B_f}{C_f}$ (variance de couleur)

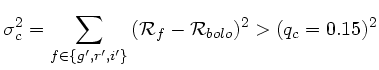
$\displaystyle \sigma_c^2 = \sum_{f \in \{g', r', i'\}}{({\cal R}_f-{\cal R}_{bolo})^2} > ( q_c = 0.15 )^2$

pour que cette extension soit dissociée du c $\oe$ ur (objet de type mixte).

$\bullet$

Ajout de la supernova :

Enfin, le décor étant posé, la vedette peut apparaître. La supernova est incontestablement une source ponctuelle, et l'on pourrait se contenter d'ajouter une composante ponctuelle à la position correspondant aux coordonnées trouvées photométriquement. Cependant, si la supernova se trouve trop proche du centre d'une galaxie apparaissant comme ponctuelle, on cherchera à extraire deux composantes gaussiennes pratiquement superposées. Les profils des composantes seront alors très corrélés, et l'algorithme d'extraction aura toute latitude d'attribuer par exemple un flux négatif à la supernova et un flux démesuré à la galaxie, la somme des deux reproduisant au mieux un eventuel profil bruité. On comprend alors qu'un fort bruit anticorrélé dominera les spectres extraits d'objets faibles et proches. Pour éviter d'extraire deux composantes dégénérées entre elles, une dernière coupure est considérée, portant sur la séparation entre le c $\oe$ ur de la galaxie hôte (la plus proche de la supernova) et la supernova, lorsque la galaxie est ponctuelle ou mixte :

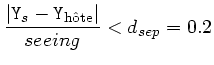
$\displaystyle \frac{\vert {\tt Y}_s-{\tt Y}_{\rm h\hat{o}te} \vert}{ seeing} < d_{sep} = 0.2$

auquel cas la supernova est fusionnée avec la galaxie hôte si cette dernière est de type ponctuel. Si la galaxie est de type mixte, on tente de conserver la décomposition supernova/galaxie en fusionnant le c $\oe$ ur et les bras de la galaxie en un profil étendu. On s'expose alors à avoir un flux négatif pour la supernova dans le bleu, qui permet de compenser la faiblesse relative du c $\oe$ ur galactique par rapport aux bras (en comparaison du profil moyen, bolométrique).

Les valeurs indiquées des 7 paramètres $N_\sigma$ = 8, = 0.75, = 0.05, $N_{\sigma B}$ = 5, $r_{b/c}$ = 0.2, = 0.15 et $d_{sep}$ =0.2 sont les valeurs par défaut, et peuvent être optionnellement modifiées pour appréhender les cas particuliers.

4.1.3.0.1

Ces opérations préliminaires de préparation des composantes à extraire sont implémentées en Python. L'extraction décrite ci-après l'est en C++.

4.1.4 Extraction guidée

Pour chaque colonne $F_k({\tt Y})=F({\tt X}_k,{\tt Y})$ du spectrogramme combiné, les profils $\mathcal{C}_i({\tt Y})$ de chacune des

composante, ponctuelle ou étendue, sont décalés de $\delta{\tt Y}_k = \alpha \times ({\tt X}_k-X_0)$ selon Y pour suivre l'inclinaison de la trace, et leur flux total est normalisé à 1.

Une composante uniforme spatialement est ajoutée pour rendre compte des résidus de soutraction du fond de ciel.

Le flux attribuable à chaque composante est estimé par minimisation du $\chi ^2$ :

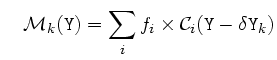
soit le modèle $\displaystyle \quad \mathcal{M}_k({\tt Y}) = \sum_i{ f_i \times \mathcal{C}_i({\tt Y}-\delta{\tt Y}_k)}$

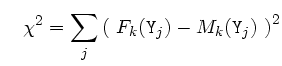
et le résidu $\displaystyle \quad \chi^2=\sum_j \left( F_k({\tt Y}_j)-M_k({\tt Y}_j) \right)^2$

La recherche des conditions annulant la dérivée du $\chi ^2$ par rapport aux mène à résoudre l'équation matricielle :

$\displaystyle \left[ \begin{array}{ccc} \sum_j \mathcal{C}_0({\tt Y}_j')^2 & \c... ...\vdots \\ \sum_j \mathcal{C}_N({\tt Y}_j')F_k({\tt Y}_j) \end{array} \right]$

où ${\tt Y}_j' = {\tt Y}_j-\delta{\tt Y}_k$ correspond au changement de variable traduisant le décalage des profils à la colonne dû à l'inclinaison de la trace.

Caractéristiques du modèle :

Les profils des composantes étendues correspondent au profil bolométrique, forcé à la positivité. Il est lissé par convolution avec une gaussienne de largeur à mi-hauteur égale à la moitié du seeing, pour en réduire le bruit sans affecter de trop sa résolution, puis suréchantillonné au centième de pixel pour pouvoir le décaler facilement selon Y par la suite. Aucune correction n'est apportée pour tenir compte de l'évolution du seeing avec $\lambda$ .

En revanche, le profil des composantes ponctuelles est une gaussienne dont le $\sigma$ varie avec $\lambda$ , selon une loi de puissance d'indice $\kappa$ = -0.3, valeur obtenue sur les spectrogrammes d'étoiles standard :

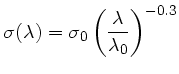
$\displaystyle \sigma(\lambda) = \sigma_0 \left( \frac{\lambda}{\lambda_0} \right)^{-0.3}$

Cette valeur diffère de celle calculée dans le cadre de la théorie des cascades turbulentes d'Andreï Nikolaïevich Kolmogorov (1941)^4.2 : -1/5, mais est identique à celle trouvée par S.Blondin lors de la réduction de spectres FORS1 de supernovæ lointaines [2].

L'extraction n'est effectuée que dans une fenêtre étroite, large de vingt fois le seeing effectif, agrandie en fonction de l'inclinaison $\alpha$ .

Next: 4.2 Limites de la Up: 4. Jouer toutes ses Previous: 4. Jouer toutes ses

Sylvain Baumont
2010-01-11