3.3 Propagation des erreurs

Après l'âge d'or de la mécanique et de la thermodynamique, où la connaissance et la prédiction semblaient ne pas avoir de bornes dans un univers obéissant à des lois physiques déterministes, vint la désillusion de la théorie quantique, probabilisant une nature incertaine. Auparavant, la notion de probabilité a été formalisée par de nombreux mathématiciens (tels Gauss, Poisson, Cauchy, Bernoulli) et son application aux sciences est devenue incontournable.

Les scientifiques s'appliquent à dévoiler la vérité par l'expérience. Le raisonnement logique et l'outil mathématique leur permettent de faire des prédictions vérifiables ou d'interpréter des observations, dans le cadre d'une théorie dont on questionne la véracité. Il n'est pas étonnant que la représentation du monde ait tellement changée au cours des âges, à mesure que les outils mathématiques et les instruments d'observations se perfectionnent. Il est cependant remarquable que ces avancées soient liées : l'émergence de nouveaux concepts physiques ouvre la voie à l'exploration de nouvelles branches des mathématiques et à des innovations technologiques, qui permettront de nouvelles expériences et la découverte de nouveaux concepts.

Comme on vient de le voir, l'interprétation des observations est limitée par le bruit de mesure, que l'on peut réduire par l'accumulation de réalisations identiques, et par la compréhension de la nature des erreurs statistiques et systématiques. Plus subtilement, l'action de la mesure a généralement un effet, même minime, sur l'objet d'étude. Ses propriétés sont modifiées par l'acte de mesurer, et la mesure n'est pas absolue. On connaît l'état de l'objet sachant qu'il est mesuré.

En bref, un diagnostic doit être accompagné de sa probabilité d'être vrai, de son incertitude, qui se calcule en propageant les erreurs connues à chaque étape de l'analyse des mesures. Le caractère aléatoire, stochastique, d'un signal se formalise par une densité de probabilité, qui décrit la probabilité que le signal prenne une valeur plutôt qu'une autre. C'est cette fonction que l'on essaye d'estimer d'après les données. Sa forme dépend du type de statistique régissant le signal, mais on l'approxime souvent par une fonction normale^3.3dont la manipulation mathématique est aisée. Le ``théorème central limite'' stipule par ailleurs que la somme de variables aléatoires indépendantes, sous des conditions de régularité, tend vers une loi normale lorsque le nombre de variables tend vers l'infini (Loi des grands nombres).

Figure 3.2: À gauche : Illustration de l'estimation d'un taux à partir de quatre mesures. Les fonctions de répartition estimées dans le cas où la loi est supposée Normale (continue), ou Poissonnienne (discrète), sont tracées. À droite : Fonction de répartition poissonniènne et son approximation gaussienne, à taux faible ( $\mu$ =4) et élevé ( $\mu$ =64).

La loi normale possède deux paramètres : sa moyenne $\mu$ et son écart-type $\sigma$ . La vraisemblance de détection d'un signal sera exprimée en nombre de $\sigma$ au dessus du fond, égal au rapport signal à bruit $\mu/\sigma$ .
Ainsi, si l'on mesure

= [18,28,21,29] gouttes de pluie par seconde, on annoncera qu'il pleut en moyenne $\mu$ = $\sum_{i=1}^4 X_i$ /4= 24 gouttes/sec, avec un écart-type de $\sigma$ = $\sum_{i=1}^4 (X_i-\mu)^2$ /4= 4.6. Ces estimées sont entachées d'erreur car on ne dispose pas d'une infinité de mesures. 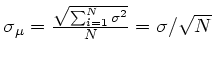L'erreur d'estimation de $\mu$ peut être elle-même estimée en supposant une loi normale, pour laquelle les incertitudes s'ajoutent quadratiquement : $\sigma_{\mu}=\frac{\sqrt{ \sum_{i=1}^N \sigma^2} }{N} = \sigma/\sqrt{N}$ =2.3. On concluera que les mesures sont en accord avec une répartition de moyenne 24.0 $\pm$ 2.3 et d'écart-type 4.6, dans l'hypothèse d'une loi normale.

Le nombre de gouttes est en fait une variable aléatoire discrète (

ne prend que des valeurs entières), qui suit une fonction de répartition Poissonnienne^3.4, dont l'unique paramètre est le taux moyen $\mu$ . Comme on le voit en Figure 3.2, pour un taux de 24, les deux lois sont proches, et quatre mesures sont loin de suffire à les différencier. La loi de Poisson s'approxime bien, pour un taux $\mu$ suffisamment grand, par une loi normale de même moyenne $\mu$ , et de même écart-type $\sqrt{\mu}$ .

Ce rappel sur l'estimation des processus stochastiques terminé, voyons comment se transcrivent ces notions dans le cas de la spectroscopie avec des capteurs CCD, et comment se formalise la propagation des bruits au cours de la calibration.

3.3.1 Un mot sur les détecteurs CCD

Dans notre cas, on ne compte pas des gouttes de pluie, mais des grains de lumière : les photons. La seule épuisette à photons que l'on connaisse est l'effet photoélectrique, qui libère des électrons que l'on sait mieux manier. Cet effet, découvert par H.R. Hertz en 1887, interprété par A. Einstein en 1905 en s'inspirant des travaux sur les quantas de M. Plank, est un exemple d'avancée des concepts scientifiques par l'expérience et le raisonnement. Un siècle après, les applications industrielles ne se comptent plus, des panneaux solaires aux capteurs numériques. Surtout, la dualité et la quantification de l'énergie des particules devint indiscutable, intronisant la théorie quantique comme ``modèle standard'' de la physique des particules.

Brièvement, les solides se distinguent électriquement en 3 catégories : les isolants, dont les électrons de valence sont liés à leur atomes, les conducteurs (ou métaux) dont les électrons de valence circulent d'un atome à l'autre, et les cristaux semi-conducteurs, dont les électrons peuvent circuler si l'on chauffe au-delà d'une certaine température.
Cette hausse d'énergie peut provenir localement d'un photon de fréquence $\nu$ , qui ait une énergie h $\nu$ suffisante pour entraîner l'électron sur une orbite conductrice, sans toutefois le détacher définitivement de la maille du cristal. L'électron part alors vers là où il y a plus de trous et moins d'électrons, et laisse un trou. Les trous se déplacent aussi, mais plus lentement.

Les Dispositifs à Charges Couplées (CCD) exploitent les propriétés des semi-conducteurs pour obtenir une bonne efficacité quantique q (nombre d'électrons libérés par photons, 0.6 < q < 0.8 e-/h $\nu$ entre 4000 et 8000 Å pour la CCD Tektronix de FORS1).

Cette efficacité quantique dépend de la longueur d'onde $\lambda$ =c/ $\nu$ des photons, et peut varier d'un pixel à un autre en raison des imperfections de manufacture. Ces variations sont reflétées dans le champ plan (variation pixel à pixel) et dans la courbe de réponse instrumentale (dépendance en $\lambda$ ).

Le circuit de lecture apporte par ailleurs un niveau de base (le piédestal), un bruit de lecture (le read out noise : RON $\sim$ 5.4 e-/pixel), et un courant d'obscurité qui remplit les pixels avec le temps ( $\sim$ 9 e-/hr/pixel pour FORS1, négligeable et négligé dans les analyses^3.5)

3.3.2 Le bruit de photons

Le flux de photons $F_0(\lambda)$ arrivant en amont de l'atmosphère terrestre obéit à une loi de Poisson : son bruit statistique s'apparente à un bruit de grenaille. La transmission atmosphérique $A(\lambda)$ , la réflectivité des miroirs et la transmission des optiques $T(\lambda)$ ainsi que l'efficacité quantique du détecteur $q(\lambda)$ tamisent ce flux. Ce tamisage conserve la nature Poissonnienne du flux d'événements, et le flux $F_{e^-}$ d'e- libérés dans le CCD s'écrit

$\displaystyle F_{e^-}(\lambda)=F_0(\lambda) A(\lambda)T(\lambda)q(\lambda)\quad [e^-]$

$\displaystyle \sigma_{e^-}(\lambda)=\sqrt{F_{e^-}(\lambda)} = \sigma_0(\lambda) \sqrt{ A(\lambda) T(\lambda) q(\lambda) }\quad [e^-]$

est directement mesurable à partir des spectrogrammes. Ceux-ci sont exprimés en ADUs, unité propre à chaque détecteur et proportionnelle aux nombre d'e- stockés par pixel. Le coefficient de proportionalité g est appelé gain du CCD ( g $\sim$ 1.46 e-/ADU pour FORS1). Ce changement d'unité, ou normalisation, ne conserve pas la nature Poissonienne du signal :

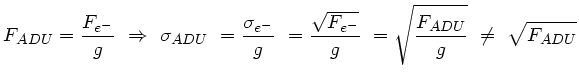
$\displaystyle F_{ADU} = \frac{F_{e^-}}{g} \Rightarrow \sigma_{ADU}\ =\frac{\... ...} =\frac{\sqrt{F_{e^-}}}{g} =\sqrt{\frac{F_{ADU}}{g}}\ \neq \sqrt{F_{ADU}}$

Le tamisage est factorisé, lors de l'analyse, en champ plan f(X $_{pix}$ , Y $_{pix}$ ) et réponse instrumentale fois le gain^3.6 $\mathcal{R}$ ( $\lambda$ )g :

$\displaystyle F_{ADU}({\tt X}_i,{\tt Y}_j)=\frac{ F_0(\lambda) f({\tt X}_i, {\t... ...}(\lambda({\tt X}_i))g}{g} =\frac{ F_{e^-}(\lambda({\tt X}_i))}{g} \quad [ADU]$

$\displaystyle \sigma_{ADU}({\tt X}_i,{\tt Y}_j)=\sigma_0(\lambda({\tt X}_i)) \... ... \frac{f({\tt X}_i, {\tt Y}_j) \mathcal{R}(\lambda({\tt X}_i))}{g}}\quad [ADU]$

On cherche à estimer

et $\sigma _0$ , en unités de flux lumineux, à partir de la mesure du flux en ADU. Les relations précédentes se réécrivent alors

$\displaystyle F_0({\tt X}_i,{\tt Y}_j) = \frac{ F_{ADU}({\tt X}_i,{\tt Y}_j) } { f({\tt X}_i, {\tt Y}_j) \mathcal{R}(\lambda({\tt X}_i)) }\quad [erg/cm^2]$

$\displaystyle \sigma_0({\tt X}_i,{\tt Y}_j) = \sqrt{F_0} = \sqrt{ \frac{F_{ADU}}{ f({\tt X}_i, {\tt Y}_j) \mathcal{R}(\lambda({\tt X}_i)) }} \quad [erg/cm^2]$

Le calcul du flux

passe aussi par la soustraction du piédestal $B_{ADU}$ et du spectre du ciel $C_{ADU}=C_{e^-}$ /g (en ADUs). Dans le cas d'un signal faible, on considère que le bruit statistique provient principalement du bruit de lecture (RON en e-) et du fond de ciel (cas d'une observation limitée par le bruit de fond). Le bruit du ciel est Poissonien ( $\sigma_{C_{e^-}}=\sqrt{C_{e^-}}$ ), et dans l'hypothèse de lois normales indépendantes, les bruits s'ajoutent quadratiquement. Ainsi, pour chaque pixel, on peut écrire le signal mesuré S et son bruit propagé $\sigma_S$ , en supposant que les modèles de piédestal, de champ plan et du spectre du ciel sont parfaits et n'introduisent pas de bruit systématique :

$\displaystyle S = \frac{F_{ADU}-B_{ADU}-C_{ADU}}{f\mathcal{R}} = \frac{S_{ADU}}{f\mathcal{R}}\quad [erg/cm^2]$

$\displaystyle \sigma_S = \frac{ \sqrt{(RON/g)^2 + C_{ADU}/g }}{f\mathcal{R}} = ... ...al{R}g}\right)^2 + \frac{C_{ADU}}{(f\mathcal{R})^2 \times g} }\quad [erg/cm^2]$

Dans le cas général, on ajoute le bruit de Poisson du signal à celui du ciel :

$\displaystyle \sigma_S = \sqrt{\left( \frac{RON}{f\mathcal{R}g}\right)^2 + \frac{C_{ADU}+S_{ADU}}{(f\mathcal{R})^2 \times g} }\quad [erg/cm^2]$

3.3.3 Savoir estimer et estimer savoir

Les formules précédentes rappellent que la qualité de l'estimation du signal et de son bruit dépendent de la qualité des modèles servant à ces estimations : piédestal B, champ plan f, réponse $\mathcal{R}$ et spectre du ciel C, mais aussi du bruit de lecture RON et du gain g pour l'estimation du bruit.

Il est donc crucial que les estimateurs mathématiques utilisés soient de bonne qualité : robustes et non-baisés. En particulier, la présence d'un impact de rayon cosmique ne doit pas affecter le résultat. La moyenne arithmétique est le meilleur estimateur d'une population pure, et l'on s'efforce donc d'épurer nos échantillons avant de les moyenner.

Cela consiste d'une part à corriger des fluctuations systématiques que l'on puisse mesurer, et d'autre part à rejeter les événements trop déviants du groupe.

La correction des fluctuations permet d'obtenir un échantillon assez homogène pour pouvoir lui appliquer l'algorithme de réjection. Ensuite, pour connaître l'amplitude des écarts acceptables, il faut disposer d'une bonne estimation du bruit statistique de l'échantillon, qui se résume à son écart-type $\sigma$ dans l'hypothèse d'une loi normale.

L'estimateur que j'ai implémenté procède à une réjection itérative des événements déviants de plus de N $\sigma$ de la médiane des événements non-rejetés (N étant un paramètre ajustable, généralement choisi à 5, ce qui rejette 0.6ppm des événements d'une population pure dont le $\sigma$ est correctement estimé). La moyenne, éventuellement pondérée, des événements valides donne l'estimation voulue. Je me réfèrerais par la suite à cet estimateur comme une moyenne robuste.

Diverses variantes sont utilisées, pour ne rejeter que les événements trop hauts, ou pour s'adapter aux propriétés statistiques de l'échantillon ( $\sigma$ identique ou propre à chaque événement, loi de Poisson avec ou sans piédestal)

L'estimateur a besoin d'information sur le bruit propre aux données d'entrée, et se doit d'en déduire la précision de son estimation. On propage ainsi les incertitudes de mesure à chaque étape de la calibration.

Notion d'ergodisme et de stationnarité :

Les processus aléatoires physiques s'étendent généralement dans l'espace et durent dans le temps (c'est le cas des gouttes de pluie). On peut donc calculer leur écart-type spatial ou temporel : la dispersion en divers lieux dans un laps de temps donné, et la dispersion à diverses époques en un même endroit respectivement.

Une variable aléatoire est dite ergodique si ses propriétés statistiques spatiales et temporelles sont identiques. Il est alors équivalent d'estimer la moyenne et l'écart-type spatialement ou temporellement.

Une variable aléatoire est dite stationnaire si sa fonction de répartition est indépendante du temps. L'estimation peut alors se faire sur n'importe quel laps de temps, et les résultats seront compatibles entre eux.

Ces deux propriétés simplifient le travail d'estimation, et sont supposées lorsque la physique sous-jacente le justifie. Dans le cas contraire, on tentera de construire des variables normalisées ayant ces propriétés.

La vérification de l'ergodisme ou de la stationnarité est intrinsèquement limitée par le nombre d'événements accessibles : si l'on veut connaître précisément la moyenne temporelle, il faut recueillir un grand nombre d'événements, donc attendre suffisamment longtemps. La résolution temporelle des mesures sera alors mauvaise. Inversement, plus on voudra suivre le détail des fluctuations temporelles, plus le nombre d'événements disponibles par intervalle de mesure sera petit, affectant la précision de la mesure. C'est une dégénérescence classique entre précision et résolution.