next up previous contents
Next: 5.4 Résultats Up: 5. L'éventail des résultats Previous: 5.2 L'heure de véritée

Sous-sections

5.3 Premières applications

Il ne faut pas perdre de vue le but dans lesquel cette procédure d'extraction dédiée a été conçue : de faciliter la classification des candidats en réduisant la contamination du spectre par la galaxie hôte. Ici encore, la conjonction des données photométrique et spectroscopique fournit l'outil le plus pertinent.

En premier lieu, ce n'est toutefois que le spectre qui puisse fournir une information cruciale : le redshift précis de la galaxie hôte du candidat. L'interprétation des courbes de lumière en dépend, et c'est un ingrédient primaire du diagramme de Hubble que le groupe du SNLS s'attache à produire.

5.3.1 Un estimateur primitif de redshift galactique : les $ \mathcal{Z}$ -let

La méthode usuelle de détermination du redshift des galaxies hôtes procède d'un ajustement visuel itératif des raies d'absorption (photosphèriques) et d'émission (nébulaires) présentes dans le spectre de la galaxie avec une librairie des raies habituelles. La raie interdite de [OII] (3727.5 Å) et le doublet du calcium CaIIH&K (3933.7 et 3968.5 Å) sont en général les marqueurs les plus proéminents.

J'ai développé un algorithme, une nouvelle fois basé sur des ondelettes, destiné à réaliser automatiquement cet ajustement sur les raies spectrales.

Choix du référenciel :

La quantité recherchée correspond à un facteur d'étirement de l'echelle des $ \lambda $ : $ F_{obs}(\lambda) = F_0(\frac{\lambda}{1+z}) $ , où F$ _{obs}$ est le flux observé, et F$ _0$ le flux émis.

Cet étirement peut être ramené à une simple translation si l'on travaille avec une variable logarithmique de $ \lambda $ , par exemple5.2 $ \mu = \log(\lambda/\lambda_0)$ :

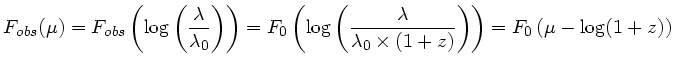
$\displaystyle F_{obs}(\mu)= F_{obs}\left(\log\left(\frac{\lambda}{\lambda_0}\ri... ...{\lambda}{\lambda_0\times(1+z)}\right)\right) = F_0\left(\mu-\log(1+z)\right) $

Ainsi, il suffit de calculer la fonction de corrélation d'une ondelette adaptée aux raies recherchées et du spectre, tout deux exprimés en fonction de $ \mu $ , et d'en trouver le maximum pour obtenir une estimation du redshift.

Construction de l'ondelette :

Exprimée dans le même référentiel logarithmique que le spectre, notre ondelette est constituée de calibres adaptés aux gaussiennes pour apréhender les raies d'émission, et de calibres adaptés aux lorentziennes pour les raies d'absorption. Rappelons que ces calibres sont proportionnels à la dérivée seconde de la fonction à calibrer, normalisés pour que leur produit soit unitaire (c.f. 3.4.4).

La largeur des raies est imposée par défaut à $ \sigma_G$ =5 Å ( $ \cong$ seeing moyen) pour les raies d'émission et $ \sigma _L$ =10 Å pour celles en absorption (originaires de photosphère plus chaudes). L'intensité relative des calibres est également imposée arbitrairement pour reproduire les rapports de raies usuellement observés (mais qui changent beaucoup d'un type de galaxie à un autre : les galaxies elliptiques n'ont pas de raies d'emission, très présentes dans les galaxies spirales). Dans la configuration par défaut, l'ondelette est plus adaptée aux galaxies à flambée d'étoiles qu'aux elliptiques.

Naturellement, le calibre correspondant à chacune des raies considérées est centré sur le $ \mu $ correspondant au $ \lambda $ de cette raie (mesuré précisément en laboratoire).

Librairie de raies spectrales :

On ne considère que les raies atomiques les plus significatives (pour les galaxies, et dans l'intervalle de $ \lambda $ couvert), regroupées par atome source. L'effet du redshift rend observables par FORS1 doté du grisme 300V les raies de $ \lambda $ inferieur à 4000 Å, mais on en trouve peu en deça de 3700 Å.

Figure: Librairie des raies de transition atomiques proéminentes dans les spectres galactiques. 9 raies de Balmer de l'Hydrogène ( de H$ \alpha $ à H$ \iota $ ) sont considérées, dont seules les 3 premières sont déclarées en émission. Les crochets (i.e. [OII]) correspondent à des transitions dites interdites, ayant un long temps de demi-vie (raies de fluorescence). La raie moléculaire de l'hydrure de magnésium (MgH) est plus large que les raies atomiques et aura une largeur $ \sigma _L$ =15 Å, contre 5 Å et 10 Å respectivement pour les raies atomiques en émission et en absorption. Les poids ont été choisis arbitrairement pour reproduire approximativement les rapports de raies d'une galaxie spirale de type Sb (semblabe à celle de 03D4ag, c.f. Figure 5.9).
\begin{figure}\begin{center} \begin{tabular}{cc} \begin{tabular}[t]{\vert l\ver... ... 3868.74 & 0.2 \\ \hline \end{tabular}\end{tabular} \end{center}\end{figure}

Procédure :

La principale difficulté de mise en \oeuvre réside dans la transposition du spectre dans le référentiel logarithmique. En effet, pour simplifier le calcul de la fonction de corrélation, il est préférable d'avoir un échantillonnage uniforme des $ \mu $ . Cependant, l'échantillonnage correspondant des $ \lambda $ ne le sera pas. D'autre part, comme on veut utiliser les fines raies spectrales, il faut conserver un échantillonnage suffisamment serré pour ne pas les émousser.

La solution retenue consiste à respecter le critère de Shannon en $ \lambda _0$ ( $ \delta\lambda = \sigma/2$ , le $ \sigma $ correspondant au plus petit du seeing et de la largeur de la fente ). On sur-échantillonne donc en deçà de $ \lambda _0$ , et l'on sous-échantillonne au-delà. Il faut donc bien choisir $ \lambda _0$ au milieu de l'intervalle spectral. Notons qu'un sur-échantillonnage sur tout l'intervalle est possible (pour $ \lambda_0 = \lambda_{max}$ ), mais mène à un nombre de points rédhibitoire.

Une fois l'échantillonnage $ \delta\mu=\delta\lambda/(\lambda_0\times\ln(10))$ défini, le spectre considéré est rééchantillonné à ce pas, grâce à un ajustement polynomial robuste d'ordre 3, effectué sur 7 points de mesures, avec une réjection à 5$ \sigma $ .

Pour un intervalle de redshift donné (de z$ _{min}$ =0.1 à z$ _{max}$ =1.2 par défaut), on construit l'ondelette de manière à englober l'ensemble des $ \mu $ nécessaires : si le spectre observé va de $ \mu_0$ à $ \mu_1$ , l'ondelette ira de $ \mu_0-\log(1+z_{max})$ à $ \mu_1-\log(1+z_{min})$ . Le pas de l'ondelette est choisi légèrement plus petit que celui du spectre ( $ \delta\lambda = \sigma/3$ ).

Enfin, pour un pas en redshift $ \delta $ z donné (0.001 par defaut), l'ondelette est décalée de $ \log$ ( z$ _{min}$ + k $ \times \delta$ z) selon $ \mu $ et son produit $ \mathcal{C}_k$ avec le spectre est calculé, k allant de 0 à (z$ _{min}$ -z$ _{max}$ )/$ \delta $ z.

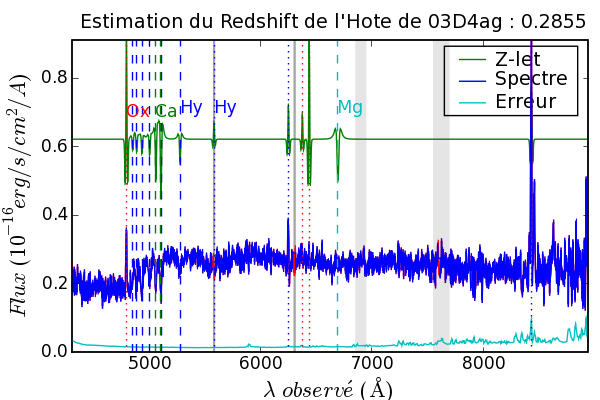
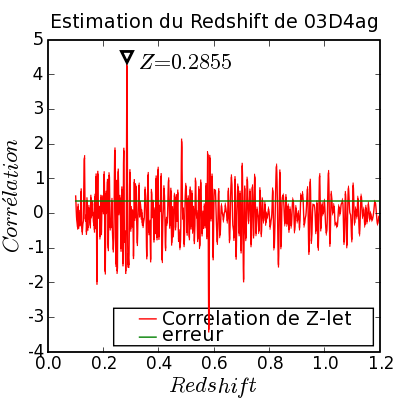
Le maximum de $ \mathcal{C}$ (z) en est déduit, fournissant une estimation du redshift du spectre considéré (c.f. Figure 5.9).

Image 03D4ag_180_zfit
Figure: Illustration de l'estimation du redshift pour la galaxie hôte de 03D4ag (En Haut). La somme des composantes coeur et bras est utilisée pour maximiser le flux et le nombre de raies. Les raies de [OII], H$ \alpha $ et H$ \beta $ sont présentes en émission. Celles de CaII et de H$ \delta $ à H$ \iota $ le sont en absorption. En revanche, les raies de H$ \gamma $ , de [OIII] et de MgH sont absentes. Les raies déclarées en èmission sont materialisées par des lignes pointillées, et celles en absorption par des tirets. La fonction de corrélation (À Droite) présente un pic significatif et pertinent à un redshift de 0.2855.
 
 Image 03D4ag_180_zlevel

Limitations :

La finesse des raies, et donc des calibres, rend la méthode sensible aux fluctuations statistiques. En particulier, les artefacts de soustraction du fond de ciel au niveau des intenses raies ionosphériques de [OI] à 5577 Å et 6300 Å sont un lieu privilégié d'accrochage de l'ondelette.

Pour en limiter l'importance, elles sont masquées à la largeur de la fente, plus une marge de deux pixels. Similairement, la profonde absorption atmosphérique de la vapeur d'eau à 7600 Å est masquée sur 20 Å.

Lorsque le niveau de signal du spectre est trop faible, une option de la ligne de commande permet d'effectuer un filtrage des points déviants de plus de N fois $ \sigma $ (N=5 par défaut) du niveau local. Cependant, ce filtrage risque d'émousser les raies les plus piquées et n'est donc pas réalisé par défaut. Si cela ne suffit pas, il est aussi possible de réduire l'intervalle de redshift de l'ajustement pour éviter un pic de corrélation aberrant.

Adaptations :

La librairie de raies, leurs largeurs et poids relatifs sont fixés arbitrairement pour fournir de bons résultats sur les galaxies spirales. Par défaut, on n'utilise que les raies de l'oxygène, de l'hydrogène, du calcium et de l'hydrure de magnésium.

Les galaxies elliptiques ne présentant pas de raies d'émission, la sélection par défaut n'est pas pertinente : les calibres en èmission, doté d'un poids important, vont accrocher sur des fluctuations statistiques.

Une option de la ligne de commande du programme de $ \mathcal{Z}$ -let permet de choisir quels atomes seront considérés pour construire l'ondelette. En général, le calcium et l'hydrure de magnésium suffisent à identifier le redshift des galaxies elliptiques.

Par défaut, lorsque la galaxie est de type mixte, la somme des deux composantes est utilisée pour maximiser le signal. Pourtant, si la composante identifée comme des bras spiraux est en réalité une galaxie de champ, le pic de corrélation risque de correspondre au redshift de cette dernière. Une autre option permet de choisir quelle composante doit être utilisée pour l'ajustement.

.

Sans adaptation particulière, environ la moitié des redshifts ainsi estimés sont corrects. Après adaptation, quasiment tous les redshifts le sont, à l'exception de quelques cas pour lesquels le signal est beaucoup trop faible (remarquons que plus le redshift est grand, moins il y a de flux et moins il y a de raies présentes dans l'intervalle spectral). Dans ce cas, l'obtention d'une estimation sûre du redshift est improbable, par quelque méthode que ce soit.

5.3.2 Classification binaire des candidats avec SALT2

Considérons maintenant le point d'orgue de tout ce travail : La classification de la source observée.

J'ai présenté dans la section 2.5 la technique usuelle d'ajustement du spectre observé par une librairie de spectres de supernova proches et de galaxies de tout types. À présent, lorsque l'extraction guidée fonctionne bien, on dispose d'un spectre non contaminé de l'objet. Ce spectre peut être comparé à la réalisation du modèle spectral de SALT2 [6] reproduisant la courbe de lumière de l'objet, pour adresser son appartenance ou non à la famille des SN-Ia.

Présentation de SALT2 :

Seconde mouture du Spectral Adaptive Lightcurve Template développé par Julien Guy pour réaliser l'ajustement des courbes de lumières des SN-Ia en vue de leur utilisation comme indicateur de distance cosmologique, SALT2 n'est plus basé sur la séquence spectrale de Nugent [11], mais sur un lot important de spectres et de courbes de lumières de SN-Ia proches et lointaines (founies par le SNLS), de manière à couvrir les phases de -10 à +50 jours autour du maximum de lumière et les $ \lambda $ de 2000 à 9200 Å.

Ce lot d'entraînement permet de construire une décomposition en composantes principales de la séquence spectrale des SN-Ia en fonction de deux paramètres intrinsèques : un avatar du stretch $ x_1$ et la couleur $ c$ :

$\displaystyle F(p,\lambda) = x_0 \times [ M_0(p,\lambda) +x_1 M_1(p,\lambda)]\times \exp[c CL(\lambda)] $

où $ p$ est la phase, $ x_0$ est la normalisation de la séquence spectrale, $ x_1$ est la valeur du premier paramètre intrinsèque (apparenté au stretch), $ c$ est la couleur de l'objet et $ CL$ est la loi moyenne de correction de couleur (d'extinction). $ x_0$ , $ x_1$ et $ c$ sont les paramètres intrinsèques à une supernova, quand les composantes principales $ M_k$ et la loi $ CL$ sont propres au modèle. La relation entre $ x_1$ et le stretch $ s_{(G01)}$ défini dans Goldhaber et al. (2001 [4]) s'écrit [6], pour -3 < $ x_1$ < 3 :

$\displaystyle s_{(G01)} = 1.07 + 0.069 x_1 -0.015 x_1^2 + 0.00067 x_1^3 $

Le modèle de courbe de lumière dans un filtre quelconque est alors directement obtenu par intégration de la séquence spectrale dans ce filtre.

Disposant de ce modèle et du redshift de l'objet, il est possible d'ajuster les courbes de lumière d'un nouvel objet dans plusieurs bandes pour en déduire la date du maximum, la magnitude visuelle au maximum (via $ x_0$ ), le stretch via $ x_1$ et la couleur $ c$ (qui définissent une séquence spectrale) reproduisant au mieux les données. La magnitude visuelle au maximum, calibrée pour corriger des corrélation avec le stretch et la couleur, fournit le module de distance de l'objet, qui compose l'axe des ordonnées du diagramme de Hubble. Un modèle d'erreur est associé au modèle spectral, normalisé de manière à ce que le $ \chi ^2$ de l'ensemble des points de mesures du lot d'entraînement soit unitaire.

Ajustement de la courbe de lumière :

Il est théoriquement possible d'ajuster simultanément la courbe de lumière et le spectre de l'objet avec SALT2, mais cette pratique s'est révélée être très instable.

La démarche choisie consiste à ajuster en premier lieu la courbe de lumière dans toutes les bandes disponibles. Les deux paramètres de SALT2 (stretch et couleur) ainsi que la date du maximum et le flux au maximum qui en sont déduits seront imposés lors de l'ajustement du spectre.

Ajustement du spectre extrait :

En raison de la forte variabilité potentielle de la fonction de réponse, ainsi que des effets de pertes de fente et de réfraction atmosphérique, l'ajustement des spectres par SALT2 autorise une renormalisation par l'exponentielle5.3d'un polynôme de bas ordre (1 par défaut, soit deux paramètres ajustables : piston $ C_0$ et couleur $ C_1$ ).

Les autres paramètres du modèle étant imposés par la courbe de lumière, cet ajustement est rapide et robuste. L'inspection visuelle du résultat d'ajustement, le $ \chi ^2$ obtenu ou l'amplitude des paramètres de normalisation sont autant d'indicateurs à la fois de la qualité de l'extraction et de la vraisemblance que l'objet soit une SN-Ia.

Cas non résolus :

Lorsque la galaxie hôte est extraite avec la supernova (composante SNGAL), on n'échappe pas à l'ajustement d'un modèle de spectre galactique. Plusieurs librairie de spectres ont été crées, en utilisant le programme de synthèse de population stellaires PEGASE [3], correspondant à divers scénarii de formation d'étoiles. Remarquons que les spectres générés par PEGASE ne contiennent pas les raies d'émission nébulaires (c.f Figure 5.10). La séquence moyenne de spectres observés de Kinney [10], déjà utilisée par le programme $ \mathcal{SN}$ -fit, permet de remédier à cette limitation lorsqu'elle se présente.

Image gal_peg_E_plot
Figure 5.10: Librairie de spectres générés par PEGASE, pour une galaxie elliptique à différents stades de sa formation. Par defaut, cette séquence est utilisée, avec 13 spectres allant de 1 milliard d'années (1 Gyr) à 13 milliards d'années par pas de 1 milliard d'années.
 

Une interpolation linéaire d'un modèle à l'autre permet de s'affranchir en partie du caractère discret de la librairie. Deux paramètres supplémentaires interviennent donc : l'indice du modèle galactique le long de la séquence choisie, et la fraction d'hôte dans le spectre. Cet ajustement de la contamination galactique permet de reproduire les couleurs du spectre extrait, ce qui rend redondant le paramètre de renormalisation $ C_1$ . Le seul paramètre $ C_0$ est donc utilisé lorsqu'une composante galactique est introduite.

Entraînement de SALT2 :

Il faut noter que SALT2 a utilisé 19 spectres VLT non contaminés de SN-Ia évidentes pour densifier son lot d'entraînement dans la partie UV de l'espace des $ \lambda $ . Il est donc abusif d'utiliser SALT2 pour classifier ces objets, ou pour valider cette procédure, mais ce sont précisément ceux dont la classification fait peu de doutes.

Figure: Exemple d'ajustement par SALT2 des courbes de lumières du candidat 04D2fp (À gauche), et du spectre extrait (À droite). Les coefficients de normalisation du spectre sont faibles ( $ C_0$ =-0,768 et $ C_1$ =-0,041). L'objet est indéniablement une SN-Ia, à un redshift de 0,416. Le spectre à été obtenu à une phase d'environ +2 jours après le maximum (ligne verticale pointillée). Le $ \chi ^2$ de l'ajustement des courbes de lumières vaut 0,99, celui du spectre vaut 1.16. La courbe pointillée, dite non calibrée, correspondant au modèle sans normalisation de couleur ( $ C_1$ =0, $ C_0$ est conservé), est ici indiscernable du modèle normalisé.

Cas d'une SN-Ia à grande
distance : 04D2fp

Image 04D2fp_NarowNeg_slit_rgb
Image 04D2fp_470_SALT2_niceLCFit Image 04D2fp_470_SALT2_niceSpecFit

Figure: Idem Fig. 5.11 pour le candidat 04D1ow. Les coefficients de normalisation du spectre vallent $ C_0$ =-1,494 et $ C_1$ =0,419. L'objet est une SN-Ia, à un redshift de 0,92. Le spectre à été obtenu à une phase d'environ +6 jours après le maximum. Le $ \chi ^2$ de l'ajustement des courbes de lumières vaut 0,94, celui du spectre vaut 0,63.

Cas d'une SN-Ia à très grande
distance : 04D1ow

Image 04D1ow_NarowNeg_slit_rgb
Image 04D1ow_683_SALT2_niceLCFit Image 04D1ow_683_SALT2_niceSpecFit

next up previous contents
Next: 5.4 Résultats Up: 5. L'éventail des résultats Previous: 5.2 L'heure de véritée
Sylvain Baumont
2010-01-11