next up previous contents
Next: 3.6 Premiers renseignements Up: 3. Les promesses de Previous: 3.4 Recettes de cuisine

Sous-sections


3.5 Digression sur le fond de ciel

Le spectre du ciel, tel qu'on le voit en figure 3.26, est composé :
$ \bullet$
d'un continuum solaire diffusée par le limbe lunaire puis par l'atmosphère (le bleu du ciel), d'autant plus intense que la lune est gibbeuse et proche de la ligne de visée,
$ \bullet$
des raies de désexcitation de l'Oxygène OI, du doublet du Sodium Na à 589 nm, et
$ \bullet$
de la pléthore de raies ro-vibrationnelles du radical Hydroxyle OH, au-delà de 6500 Å, prépondérentes dans l'IR.

Il a déjà été dit que la soustraction du spectre du ciel était la principale source d'erreur systématique. Elle est visible sur le spectrogramme combiné (c.f. Fig 3.26), à l'endroit des raies de l'OI (à 5577 Å et 6300 Å). Ces raies étant systématiquement intenses, et leur soustraction parfois approximative, on aimerait appliquer un traitement spécifique pour ce résidu.

Son origine est liée à la qualité du modèle de spectre du ciel, et à celle des coefficients de dispersion. Le spectre du ciel est estimé à $ \pm $ 100 pixels autour de la source, dans des bandes de 200 pixels de large. Sa soustraction doit donc être bonne en $ Y_{s} \pm$ 100 pixels, mais aussi mauvaise en $ Y_{s}$ qu'en $ Y_{s} \pm$ 200 pixels.

3.5.1 Où estimer le spectre du ciel

En raison de la courbure des raies et de l'estimation par colonnes, nos spectres projetés par bande ne pourront être que plus larges qu'en réalité. Le moyennage robuste limite cet effet en ne gardant qu'un sous-groupe médian lorsque l'échantillon est bi-modal, et en passant fluidement d'un mode à l'autre.

Plus les bandes sont étroites, moins cet élargissement est grand, mais plus le bruit résiduel est important. Il faut donc trouver un compromis sur la largeur des bandes. Au centre, où la distorsion est faible, une largeur de 200 lignes s'est avérée être un bon choix.

On pourrait penser utiliser des bandes couvrant l'ensemble de l'image pour construire le modèle du spectre du ciel, mais cela se heurte à la dégradation de l'image aux bords (élargissement de la PSF, donc de l'image des raies). C'est la raison pour laquelle le modèle du spectre du ciel finalement soustrait est estimé dans des bandes adjacentes à la source, pour que son profil soit le plus proche possible de celui qui se trouve à la position de la source.

Il reste encore un effet subtil : la pixelisation du spectre réel. En fonction de l'échantillonnage -de l'intégration- opérée par les pixels sur le spectre supposé spatialement uniforme, le profil discret obtenu varie. On ne connaît donc que le spectre intégré dans les pixels. Comme c'est ce que l'on veut soustraire, ce n'est pas critique. Seulement, le modèle ne sera précis que pour les positions relatives de l'échelle des pixels, et de celle des $ \lambda $ , valables dans la bande d'estimation. Pour des décalages différents, la valeur du modèle n'est qu'une interpolation. Ainsi, pour une raie, si le centre de la raie se trouve toujours entre X=$ X_{0}$ -0.1 et X=$ X_{0}$ +0.1 du bas au haut des bandes, et qu'il se trouve à X=$ X_{0}$ -0.15 en $ Y_{s}$ , le spectre discretisé du ciel en $ Y_{s}$ risque d'être différent de l'interpolation moyenne échantillonnée selon les $ \lambda({\tt X}, Y_{s})$ .

Ceci est d'autant plus sensible que le spectre réel du ciel est structuré : lorsque sa dérivée est grande, aux limites des raies intenses, là précisément où l'interpolation se fait sentir. En particulier, on doit s'attendre à des effets de diffraction, d'interférences qui modifieront le profil carré des raies prévu géométriquement, pour faire apparaître des figures de diffraction de trame sub-pixelaire (c.f. Fig 3.28). Le contraste de ces figures dépend de la cohérence spatiale et temporelle de l'émission du ciel, sûrement corrélée au seeing, et leur pas dépend de l'angle d'ouverture du faisceau incident sur le CCD.

Figure 3.28: À gauche : Effet de la diffraction sur l'image d'une fente, pour une illumination cohérente ou incohérente, et de la pixelisation. À droite : image théorique à haute résolution d'une fente en lumière cohérente (haut), et son image pixélisée (bas).
Image slit_10_diffract
Image slit_coherent
Image slit_pixelized

3.5.2 Effet de la diffraction

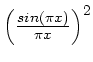Les images ne permettent pas de trouver cette structure sub-pixelaire, mais la théorie de la diffraction peut la prévoir. Dans une hypothèse simplificatrice, l'image d'un point source (sa tâche d'Airy, ou sa PSF idéale de diffraction) par un instrument de distance focale $ f$ et de diamètre $ D$ est un sinus cardinal au carré $ \left(\frac{sin(\pi x)}{\pi x}\right)^2$ , avec $ x=\frac{ X D}{\lambda f}$ (son intensité, égale au carré de l'amplitude du champ électrique de l'onde). L'image d'une fente par une lumière incohérente est simplement la convolution de la fonction porte de la fente par ce sinus cardinal au carré. Dans le cas d'une lumière cohérente, l'intensité de l'image est cette fois le carré de la convolution de la fonction porte avec l'amplitude de la PSF : avec un sinus cardinal. On voit en figure 3.28 la différence entre ces deux cas pour une fente de 1.0'', une focale de 108 m et un diamètre de 8.2 m.

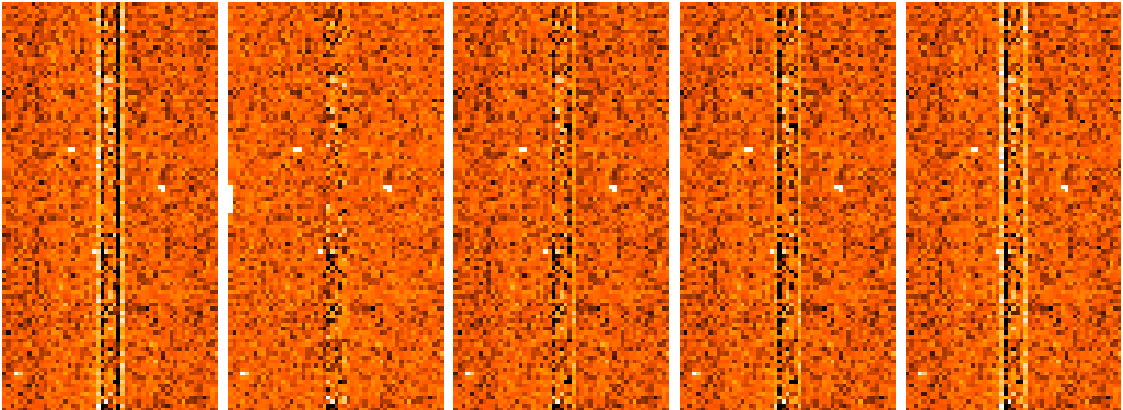
Si l'on tente à présent de soustraire un tel profil, plus ou moins cohérent, d'un spectrogramme calibré du CCD, on obtient les images présentées en figure 3.29. La région correspond à la position de la raie de OI, et à la position de l'axe optique (là où $ \frac{d\lambda}{dy}$ =0, soit en $ y=-\frac{C_y}{2 C_{y2}}$ ; ou en Y=1020 ici). La position des profils théoriques est estimé via un filtrage par ondelette en chapeau Mexicain du profil projeté dans cette même région. Pour comparaison, on trouvera aussi le résultat de la soustraction d'un profil carré pixelisé et du profil estimé par moyenne robuste selon Y (sur 100 pixels) et interpolé : le profil projeté.

Figure 3.29: Soustraction d'un profil carré pixelisé (a), du profil projeté (b), et d'un profil théorique de diffraction, en supposant une illumination incohérente (c), mi-cohérente (d) et cohérente (e). L'image brute choisie est le troisième spectrogramme de la série.
Image allOIsub

Dans ce cas favorable (distorsion minimale), on constate que la soustraction du profil projeté est la plus efficace. L'ajout de la diffraction améliore la soustraction par rapport à un profil de raie théorique géométrique, mais la structure fine de diffraction est assurément plus complexe que le modèle simplifié utilisé pour cette étude (qui oublie le collimateur. L'interfrange $ \frac{\lambda f}{D}$ serait 5 fois moindre).

La quantification des résidus de soustraction au niveau des bords de la raie permet de remonter à l'imprécision sur l'intensité, sur la position et sur la largeur de la raie, ouvrant la voie à un traitement iteratif similaire à celui présenté pour les raies photosphériques des étoiles standard. Toutefois, en l'absence de modèle adéquat de diffraction (et, en particulier, de cohérence), la soustraction individuelle des raies n'est pas satisfaisante. L'amplitude des pires résidus est de l'ordre de 30 ADUs pour une raie d'intensité 650 ADUs, soit moins de 5%, et la fraction de la couverture spectrale polluée est aussi inférieure au %.

En conséquence, on se bornera à soustraire le profil projeté moyenné par bandes, en ayant pris soin de bien choisir la largeur des bandes pour limiter l'élargissement du profil estimé. Les éventuels résidus dûs à une structure fine des raies seront isolés lors de l'extraction, pour peu qu'ils soient assez uniformes dans l'étroite fenêtre d'extraction.

next up previous contents
Next: 3.6 Premiers renseignements Up: 3. Les promesses de Previous: 3.4 Recettes de cuisine
Sylvain Baumont
2010-01-11